题目内容
【题目】某机构为了调查某市同时符合条件![]() 与
与![]() (条件
(条件![]() :营养均衡,作息规律;条件
:营养均衡,作息规律;条件![]() :经常锻炼,劳逸结合)的高中男生的体重
:经常锻炼,劳逸结合)的高中男生的体重![]() (单位:
(单位:![]() )与身高
)与身高![]() (单位:
(单位: ![]() )是否存在较好的线性关系,该机构搜集了
)是否存在较好的线性关系,该机构搜集了![]() 位满足条件的高中男生的数据,得到如下表格:
位满足条件的高中男生的数据,得到如下表格:
身高/ |
|
|
|
|
|
|
体重/ |
|
|
|
|
|
|
根据表中数据计算得到![]() 关于
关于![]() 的线性回归方程对应的直线的斜率为
的线性回归方程对应的直线的斜率为![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到整数部分);
精确到整数部分);
(2)已知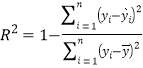 ,且当
,且当![]() 时,回归方程的拟合效果较好。试结合数据
时,回归方程的拟合效果较好。试结合数据![]() ,判断(1)中的回归方程的拟合效果是否良好?
,判断(1)中的回归方程的拟合效果是否良好?
(3)该市某高中有![]() 位男生同时符合条件
位男生同时符合条件![]() 与
与![]() ,将这
,将这![]() 位男生的身高(单位:
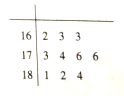
位男生的身高(单位:![]() )的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这
)的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这![]() 位男生的体重未超过
位男生的体重未超过![]() 的所有男生体重(单位:
的所有男生体重(单位:![]() )的平均数(结果精确到整数部分).
)的平均数(结果精确到整数部分).
【答案】(1) ![]() .
.
(2)(1)中的回归方程的拟合效果良好.
(3)![]() .
.
【解析】分析:(1)由线性回归方程对应的直线的斜率得![]() ,再求均值,再根据
,再求均值,再根据![]() 求
求![]() ,(2)计算
,(2)计算![]() ,与0.9比较确定拟合效果,(3)先根据线性回归方程确定未超过
,与0.9比较确定拟合效果,(3)先根据线性回归方程确定未超过![]() 的所有男生体重,再计算均值,最后代入线性回归方程得结果.
的所有男生体重,再计算均值,最后代入线性回归方程得结果.
详解:(1)依题意可知![]() ,
,
∵![]() ,
,
∴![]() ,
,
故![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() .
.
(2)∵![]()
![]()
∴ ,
,
故(1)中的回归方程的拟合效果良好.
(3)令![]() ,得
,得![]() ,
,
故这![]() 位男生中未超过
位男生中未超过![]() 的所有男生的身高(单位:
的所有男生的身高(单位:![]() )为
)为![]()
这![]() 为男生体重的平均数
为男生体重的平均数![]()
故这![]() 位男生中体重未超过
位男生中体重未超过![]() 的所有男生体重的平均数为
的所有男生体重的平均数为![]() .
.

【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位:![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
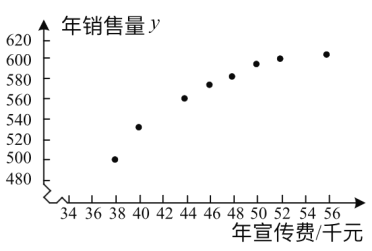
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 298.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)以知这种产品的年利率![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据(2)的结果求年宣传费
.根据(2)的结果求年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
附:对于一组数据![]() ,
,![]() ……
……![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()
