МвДїДЪИЭ
ЎѕМвДїЎїДі№«ЛѕОЄИ·¶ЁПВТ»Дк¶ИН¶ИлДіЦЦІъЖ·µДРыґ«·СЈ¬РиБЛЅвДкРыґ«·С![]() ЈЁµҐО»ЈєЗ§ФЄЈ©¶ФДкПъКЫБї
ЈЁµҐО»ЈєЗ§ФЄЈ©¶ФДкПъКЫБї![]() ЈЁµҐО»Јє
ЈЁµҐО»Јє![]() Ј©єНДкАыИу
Ј©єНДкАыИу![]() ЈЁµҐО»ЈєЗ§ФЄЈ©µДУ°ПмЈ¬¶ФЅь8ДкµДДкРыґ«·С
ЈЁµҐО»ЈєЗ§ФЄЈ©µДУ°ПмЈ¬¶ФЅь8ДкµДДкРыґ«·С![]() єНДкПъКЫБї
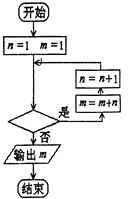
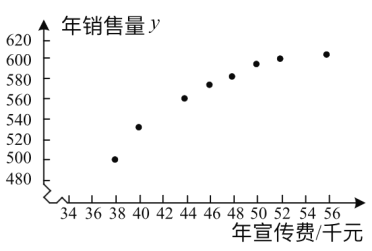
єНДкПъКЫБї![]() КэѕЭЧчБЛіхІЅґ¦АнЈ¬µГµЅПВГжµДЙўµгНјј°Т»Р©НіјЖБїµДЦµ.
КэѕЭЧчБЛіхІЅґ¦АнЈ¬µГµЅПВГжµДЙўµгНјј°Т»Р©НіјЖБїµДЦµ.
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 298.8 | 1.6 | 1469 | 108.8 |
±нЦР![]() Ј¬
Ј¬![]()
ЈЁ1Ј©ёщѕЭЙўµгНјЕР¶ПЈ¬![]() Ул
Ул![]() ДДТ»ёцККТЛЧчОЄДкПъКЫБї
ДДТ»ёцККТЛЧчОЄДкПъКЫБї![]() №ШУЪДкРыґ«·С
№ШУЪДкРыґ«·С![]() µД»Ш№й·ЅіМАаРНЈїЈЁёшіцЕР¶ПјґїЙЈ¬І»±ШЛµГчАнУЙЈ©
µД»Ш№й·ЅіМАаРНЈїЈЁёшіцЕР¶ПјґїЙЈ¬І»±ШЛµГчАнУЙЈ©
ЈЁ2Ј©ёщѕЭЈЁ1Ј©µДЕР¶ПЅб№ыј°±нЦРКэѕЭЈ¬ЅЁБў![]() №ШУЪ
№ШУЪ![]() µД»Ш№й·ЅіМЈ»
µД»Ш№й·ЅіМЈ»
ЈЁ3Ј©ТФЦЄХвЦЦІъЖ·µДДкАыВК![]() Ул
Ул![]() Ўў
Ўў![]() µД№ШПµОЄ
µД№ШПµОЄ![]() .ёщѕЭЈЁ2Ј©µДЅб№ыЗуДкРыґ«·С
.ёщѕЭЈЁ2Ј©µДЅб№ыЗуДкРыґ«·С![]() К±Ј¬ДкПъКЫБїј°ДкАыИуµДФ¤±ЁЦµКЗ¶аЙЩЈї
К±Ј¬ДкПъКЫБїј°ДкАыИуµДФ¤±ЁЦµКЗ¶аЙЩЈї
ёЅЈє¶ФУЪТ»ЧйКэѕЭ![]() Ј¬
Ј¬![]() ЎЎ
ЎЎ![]() Ј¬Жд»Ш№йПЯ
Ј¬Жд»Ш№йПЯ![]() µДР±ВКєНЅШѕаµДЧоРЎ¶юіЛ№АјЖ·Ц±рОЄЈє
µДР±ВКєНЅШѕаµДЧоРЎ¶юіЛ№АјЖ·Ц±рОЄЈє Ј¬
Ј¬![]()
Ўѕґр°ёЎї(1) ![]() ККТЛЧчОЄДкПъКЫБї
ККТЛЧчОЄДкПъКЫБї![]() №ШУЪДкРыґ«·С
№ШУЪДкРыґ«·С![]() µД»Ш№й·ЅіМАаРН. (2)
µД»Ш№й·ЅіМАаРН. (2) ![]() (3)66.32
(3)66.32
ЎѕЅвОцЎї
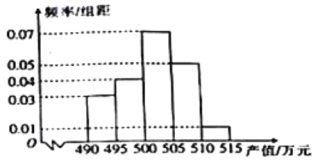
(1)ёщѕЭНјРОїЙЦЄСЎФсЗъПЯёьјУ·ыєПЈ»
ЈЁ2Ј©НЁ№эЧоРЎ¶юіЛ·ЁјЖЛгјґїЙµГµЅ»Ш№й·ЅіМЈ»
ЈЁ3Ј©ХТµЅzєНxµДєЇКэЈ¬ЧЄ»ЇОЄ¶юґОєЇКэјґїЙµГµЅЧоЦµ.
ЅвЈєЈЁ1Ј©УЙЙўµгНјїЙТФЕР¶ПЈ¬![]() ККТЛЧчОЄДкПъКЫБї
ККТЛЧчОЄДкПъКЫБї![]() №ШУЪДкРыґ«·С
№ШУЪДкРыґ«·С![]() µД»Ш№й·ЅіМАаРН.
µД»Ш№й·ЅіМАаРН.
ЈЁ2Ј©Бо![]() Ј¬ПИЅЁБў
Ј¬ПИЅЁБў![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ.УЙУЪ
µДПЯРФ»Ш№й·ЅіМ.УЙУЪ
 Ј¬
Ј¬![]() .
.
ЛщТФ![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМОЄ
µДПЯРФ»Ш№й·ЅіМОЄ![]() Ј¬
Ј¬
ТтґЛ![]() №ШУЪ
№ШУЪ![]() µД»Ш№й·ЅіМОЄ
µД»Ш№й·ЅіМОЄ![]() .
.
ЈЁ3Ј©ЈЁiЈ©УЙЈЁIIЈ©ЦЄЈ¬µ±![]() К±Ј¬ДкПъКЫБї
К±Ј¬ДкПъКЫБї![]() µДФ¤±ЁЦµ
µДФ¤±ЁЦµ![]()
ДкАыИу![]() µДФ¤±ЁЦµ
µДФ¤±ЁЦµ![]() .
.

ЎѕМвДїЎїДіКРґУёЯ¶юДкј¶Лж»ъСЎИЎ1000ГыС§ЙъЈ¬НіјЖЛыГЗСЎРЮОпАнЎў»ЇС§ЎўЙъОпЎўХюЦОЎўАъК·єНµШАнБщГЕїОіМЈЁЗ°3ГЕОЄАнїЖїОіМЈ¬єу3ГЕОЄОДїЖїОіМЈ©µДЗйїцЈ¬µГµЅИзПВНіјЖ±нЈ¬ЖдЦРЎ°ЎМЎ±±нКѕСЎїОЈ¬Ў°їХ°ЧЎ±±нКѕОґСЎЈ®
·Ѕ°ё ИЛКэ | ОпАн | »ЇС§ | ЙъОп | ХюЦО | АъК· | µШАн | |
Т» | 220 | ЎМ | ЎМ | ЎМ | |||
¶ю | 200 | ЎМ | ЎМ | ЎМ | |||
Иэ | 180 | ЎМ | ЎМ | ЎМ | |||
ЛД | 175 | ЎМ | ЎМ | ЎМ | |||
Ое | 135 | ЎМ | ЎМ | ЎМ | |||
Бщ | 90 | ЎМ | ЎМ | ЎМ | |||
ЈЁўсЈ©ФЪХв1000ГыС§ЙъЦРЈ¬ґУСЎРЮОпАнµДС§ЙъЦРЛж»ъСЎИЎ1ИЛЈ¬ЗуёГС§ЙъСЎРЮХюЦОµДёЕВКЈ»
ЈЁўтЈ©ФЪХв1000ГыС§ЙъЦРЈ¬ґУСЎФс·Ѕ°ёТ»Ўў¶юЎўИэµДС§ЙъЦРёчСЎИЎ2ГыС§ЙъЈ¬Из№ыФЪХв6ГыС§ЙъЦРЛж»ъСЎИЎ2ГыЈ¬ЗуХв2ГыС§ЙъіэСЎРЮОпАнТФНвБнНвБЅГЕСЎїОЦРУРПаН¬їЖДїµДёЕВКЈ»
ЈЁўуЈ©АыУГ±нЦРКэѕЭ№АјЖёГКРСЎїОЖ«ОДЈЁјґСЎРЮЦБЙЩБЅГЕОДїЖїОіМЈ©µДС§ЙъИЛКэ¶а»№КЗЖ«АнЈЁјґСЎРЮЦБЙЩБЅГЕАнїЖїОіМЈ©µДС§ЙъИЛКэ¶аЈ¬ІўЛµГчАнУЙ.
ЎѕМвДїЎїДі»ъ№№ОЄБЛµчІйДіКРН¬К±·ыєПМхјю![]() Ул
Ул![]() (Мхјю
(Мхјю![]() ЈєУЄСшѕщєвЈ¬ЧчПў№жВЙЈ»Мхјю
ЈєУЄСшѕщєвЈ¬ЧчПў№жВЙЈ»Мхјю![]() ЈєѕіЈ¶НБ¶Ј¬АНТЭЅбєП)µДёЯЦРДРЙъµДМеЦШ
ЈєѕіЈ¶НБ¶Ј¬АНТЭЅбєП)µДёЯЦРДРЙъµДМеЦШ![]() (µҐО»:
(µҐО»:![]() )УлЙнёЯ
)УлЙнёЯ![]() (µҐО»:
(µҐО»: ![]() )КЗ·сґжФЪЅПєГµДПЯРФ№ШПµЈ¬ёГ»ъ№№ЛСјЇБЛ
)КЗ·сґжФЪЅПєГµДПЯРФ№ШПµЈ¬ёГ»ъ№№ЛСјЇБЛ![]() О»ВъЧгМхјюµДёЯЦРДРЙъµДКэѕЭЈ¬µГµЅИзПВ±нёс:
О»ВъЧгМхјюµДёЯЦРДРЙъµДКэѕЭЈ¬µГµЅИзПВ±нёс:
ЙнёЯ/ |
|
|
|
|
|
|
МеЦШ/ |
|
|
|
|
|
|
ёщѕЭ±нЦРКэѕЭјЖЛгµГµЅ![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ¶ФУ¦µДЦ±ПЯµДР±ВКОЄ
µДПЯРФ»Ш№й·ЅіМ¶ФУ¦µДЦ±ПЯµДР±ВКОЄ![]() .
.
(1)Зу![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() (
(![]() ѕ«И·µЅХыКэІї·Ц)Ј»
ѕ«И·µЅХыКэІї·Ц)Ј»
(2)ТСЦЄ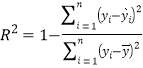 Ј¬ЗТµ±
Ј¬ЗТµ±![]() К±Ј¬»Ш№й·ЅіМµДДвєПР§№ыЅПєГЎЈКФЅбєПКэѕЭ
К±Ј¬»Ш№й·ЅіМµДДвєПР§№ыЅПєГЎЈКФЅбєПКэѕЭ![]() Ј¬ЕР¶П(1)ЦРµД»Ш№й·ЅіМµДДвєПР§№ыКЗ·сБјєГЈї
Ј¬ЕР¶П(1)ЦРµД»Ш№й·ЅіМµДДвєПР§№ыКЗ·сБјєГЈї
(3)ёГКРДіёЯЦРУР![]() О»ДРЙъН¬К±·ыєПМхјю
О»ДРЙъН¬К±·ыєПМхјю![]() Ул
Ул![]() Ј¬Ѕ«Хв
Ј¬Ѕ«Хв![]() О»ДРЙъµДЙнёЯ(µҐО»:
О»ДРЙъµДЙнёЯ(µҐО»:![]() )µДКэѕЭ»жЦЖіЙИзПВµДѕҐТ¶НјЎЈАыУГЈЁ1Ј©ЦРµД»Ш№й·ЅіМ№АјЖХв
)µДКэѕЭ»жЦЖіЙИзПВµДѕҐТ¶НјЎЈАыУГЈЁ1Ј©ЦРµД»Ш№й·ЅіМ№АјЖХв![]() О»ДРЙъµДМеЦШОґі¬№э
О»ДРЙъµДМеЦШОґі¬№э![]() µДЛщУРДРЙъМеЦШЈЁµҐО»Јє
µДЛщУРДРЙъМеЦШЈЁµҐО»Јє![]() Ј©µДЖЅѕщКэЈЁЅб№ыѕ«И·µЅХыКэІї·ЦЈ©.
Ј©µДЖЅѕщКэЈЁЅб№ыѕ«И·µЅХыКэІї·ЦЈ©.
ЎѕМвДїЎїДіЕ©їЖЛщ¶Ф¶¬јѕЦзТ№ОВІоґуРЎУлДі·ґјѕЅЪґу¶№РВЖ·ЦЦ·ўСї¶аЙЩЦ®јдµД№ШПµЅшРР·ЦОцСРѕїЈ¬ЛыГЗ·Ц±рјЗВјБЛ![]() ФВ
ФВ![]() ИХЦБ
ИХЦБ![]() ФВ
ФВ![]() ИХµДГїМмЦзТ№ОВІоУлКµСйКТГїМмГї
ИХµДГїМмЦзТ№ОВІоУлКµСйКТГїМмГї![]() їЕЦЦЧУЦРµД·ўСїКэЈ¬µГµЅИзПВЧКБПЈє
їЕЦЦЧУЦРµД·ўСїКэЈ¬µГµЅИзПВЧКБПЈє
ИХЖЪ |
|
|
|
|
|
ОВІо |
|
|
|
|
|
·ўСїКэ |
|
|
|
|
|
ёГЕ©їЖЛщИ·¶ЁµДСРѕї·Ѕ°ёКЗЈєПИґУХв![]() ЧйКэѕЭЦРСЎИЎ
ЧйКэѕЭЦРСЎИЎ![]() ЧйЈ¬УГКЈПВµД
ЧйЈ¬УГКЈПВµД![]() ЧйКэѕЭЗуПЯРФ»Ш№й·ЅіМЈ¬ФЩ¶Ф±»СЎИЎµД
ЧйКэѕЭЗуПЯРФ»Ш№й·ЅіМЈ¬ФЩ¶Ф±»СЎИЎµД![]() ЧйКэѕЭЅшРРјмСй.
ЧйКэѕЭЅшРРјмСй.
ЈЁ1Ј©ЗуСЎИЎµД![]() ЧйКэѕЭЗЎєГКЗІ»ПаБЪБЅМмКэѕЭµДёЕВКЈ»
ЧйКэѕЭЗЎєГКЗІ»ПаБЪБЅМмКэѕЭµДёЕВКЈ»
ЈЁ2Ј©ИфСЎИЎµДКЗ![]() ФВ
ФВ![]() ИХУл
ИХУл![]() ФВ
ФВ![]() ИХµДКэѕЭЈ¬ЗлёщѕЭ
ИХµДКэѕЭЈ¬ЗлёщѕЭ![]() ФВ
ФВ![]() ИХЦБ
ИХЦБ![]() ФВ
ФВ![]() ИХµДКэѕЭЗуіц
ИХµДКэѕЭЗуіц![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() Ј»
Ј»
ЈЁ3Ј©ИфУЙПЯРФ»Ш№й·ЅіМµГµЅµД№АјЖКэѕЭУлЛщСЎіцµДјмСйКэѕЭµДОуІоѕщІ»і¬№э![]() їЕ.ФтИПОЄµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµД.КФОКЈЁ2Ј©ЦРЛщµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµДВрЈї
їЕ.ФтИПОЄµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµД.КФОКЈЁ2Ј©ЦРЛщµГµЅµДПЯРФ»Ш№й·ЅіМКЗїЙїїµДВрЈї
ёЅЈє»Ш№йЦ±ПЯµДР±ВКєНЅШѕаµДЧоРЎ¶юіЛ№АјЖ№«КЅ·Ц±рОЄЈє
 Ј¬
Ј¬![]() .
.