题目内容
【题目】某校高一年级开设![]() 五门选修课,每位同学须彼此独立地从中选择两门课程,已知甲同学必选
五门选修课,每位同学须彼此独立地从中选择两门课程,已知甲同学必选![]() 课程,乙同学不选
课程,乙同学不选![]() 课程,丙同学从五门课程中随机任选两门.
课程,丙同学从五门课程中随机任选两门.
(1)求甲同学与乙同学恰有一门课程相同的概率;
(2)设![]() 为甲、乙、丙三位同学中选
为甲、乙、丙三位同学中选![]() 课程的人数,求
课程的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(1)甲同学必选![]() 课程,乙同学不选
课程,乙同学不选![]() 课程,丙同学从五门课程中随机任选两门共有
课程,丙同学从五门课程中随机任选两门共有![]() 种情况,甲同学与乙同学恰有一门课程相同共有
种情况,甲同学与乙同学恰有一门课程相同共有![]() 种情况,由古典概型概率公式可得结果;(2)
种情况,由古典概型概率公式可得结果;(2)![]() 的可能取值为
的可能取值为![]() ,结合组合知识,利用古典概型概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得
,结合组合知识,利用古典概型概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
详解:(1)分两种情况讨论:①甲选择![]() 课程,则乙只能选
课程,则乙只能选![]() ,并从
,并从![]() 中再选一门,共
中再选一门,共![]() 种.
种.
②甲选择![]() 课程,并从
课程,并从![]() 中任选一门,则乙只能一门与甲同,另一门与甲不同,
中任选一门,则乙只能一门与甲同,另一门与甲不同,
则有![]() 种.
种.
故所求概率为![]() ;
;
(2)分别讨论三人即可.
![]() ,即都不选,则有:
,即都不选,则有:![]() .
.
![]() ,即甲选,乙选,或丙选,则有:
,即甲选,乙选,或丙选,则有:![]() .
.
![]() ,即都选,则:
,即都选,则:![]()
![]()
所以其分布列如下:
|
|
|
|
|
|
|
|
|
|
则![]() .
.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案【题目】某机构为了调查某市同时符合条件![]() 与
与![]() (条件
(条件![]() :营养均衡,作息规律;条件
:营养均衡,作息规律;条件![]() :经常锻炼,劳逸结合)的高中男生的体重
:经常锻炼,劳逸结合)的高中男生的体重![]() (单位:
(单位:![]() )与身高
)与身高![]() (单位:
(单位: ![]() )是否存在较好的线性关系,该机构搜集了
)是否存在较好的线性关系,该机构搜集了![]() 位满足条件的高中男生的数据,得到如下表格:
位满足条件的高中男生的数据,得到如下表格:
身高/ |
|
|
|
|
|
|
体重/ |
|
|
|
|
|
|
根据表中数据计算得到![]() 关于
关于![]() 的线性回归方程对应的直线的斜率为
的线性回归方程对应的直线的斜率为![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到整数部分);
精确到整数部分);
(2)已知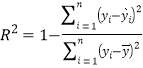 ,且当
,且当![]() 时,回归方程的拟合效果较好。试结合数据
时,回归方程的拟合效果较好。试结合数据![]() ,判断(1)中的回归方程的拟合效果是否良好?
,判断(1)中的回归方程的拟合效果是否良好?
(3)该市某高中有![]() 位男生同时符合条件
位男生同时符合条件![]() 与
与![]() ,将这
,将这![]() 位男生的身高(单位:
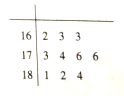
位男生的身高(单位:![]() )的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这
)的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这![]() 位男生的体重未超过
位男生的体重未超过![]() 的所有男生体重(单位:
的所有男生体重(单位:![]() )的平均数(结果精确到整数部分).
)的平均数(结果精确到整数部分).
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了![]() 月
月![]() 日至
日至![]() 月
月![]() 日的每天昼夜温差与实验室每天每
日的每天昼夜温差与实验室每天每![]() 颗种子中的发芽数,得到如下资料:
颗种子中的发芽数,得到如下资料:
日期 |
|
|
|
|
|
温差 |
|
|
|
|
|
发芽数 |
|
|
|
|
|
该农科所确定的研究方案是:先从这![]() 组数据中选取
组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再对被选取的
组数据求线性回归方程,再对被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是不相邻两天数据的概率;
组数据恰好是不相邻两天数据的概率;
(2)若选取的是![]() 月
月![]() 日与
日与![]() 月
月![]() 日的数据,请根据
日的数据,请根据![]() 月
月![]() 日至
日至![]() 月
月![]() 日的数据求出
日的数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 颗.则认为得到的线性回归方程是可靠的.试问(2)中所得到的线性回归方程是可靠的吗?
颗.则认为得到的线性回归方程是可靠的.试问(2)中所得到的线性回归方程是可靠的吗?
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.