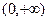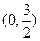题目内容
设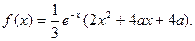
(1)求a的值,使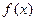 的极小值为0;
的极小值为0;
(2)证明:当且仅当a=3时,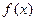 的极大值为4。
的极大值为4。
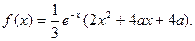
(1)求a的值,使
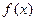 的极小值为0;
的极小值为0;(2)证明:当且仅当a=3时,
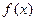 的极大值为4。
的极大值为4。(1)当a=0或a=2时,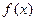 的极小值为0(2)见解析
的极小值为0(2)见解析
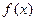 的极小值为0(2)见解析
的极小值为0(2)见解析 (1)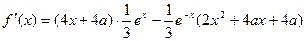
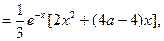
令 时,无极值。
时,无极值。
(1)当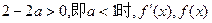 的变化情况如下表(一)
的变化情况如下表(一)
此时应有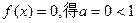
(2)当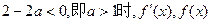 的变化情况如下表(二)
的变化情况如下表(二)
此时应有

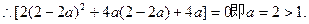
综上所述,当a=0或a=2时,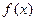 的极小值为0。
的极小值为0。
(2)由表(一)(二)知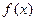 取极大值有两种可能。
取极大值有两种可能。
由表(一)应有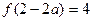 ,
,
即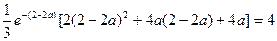

则
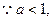
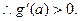 此时g(a)为增函数,
此时g(a)为增函数,
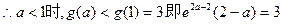 不能成立。
不能成立。
若a>1,由表(二)知,应有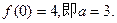
综上所述,当且仅当a=3时,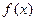 有极大值4。
有极大值4。
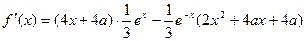
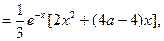
令
 时,无极值。
时,无极值。(1)当
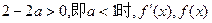 的变化情况如下表(一)
的变化情况如下表(一)| x | (-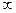 ,0) ,0) | 0 | (0,2-2a) | 2-2a | (2-2a,+ 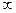 ) ) |
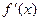 | - | 0 | + | 0 | - |
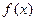 | ↘ | 极小值 | ↗ | 极大值 | ↘ |
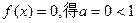
(2)当
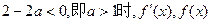 的变化情况如下表(二)
的变化情况如下表(二)| x | (-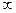 ,2-2a) ,2-2a) | 2-2a | (2-2a,0) | 0 | (0+ 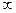 ) ) |
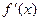 | - | 0 | + | 0 | - |
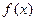 | ↘ | 极小值 | ↗ | 极大值 | ↘ |


综上所述,当a=0或a=2时,
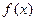 的极小值为0。
的极小值为0。(2)由表(一)(二)知
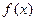 取极大值有两种可能。
取极大值有两种可能。由表(一)应有
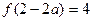 ,
,即
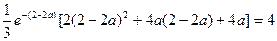

则

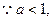
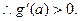 此时g(a)为增函数,
此时g(a)为增函数,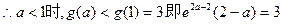 不能成立。
不能成立。若a>1,由表(二)知,应有
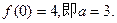
综上所述,当且仅当a=3时,
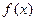 有极大值4。
有极大值4。
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
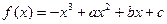 图象上的点
图象上的点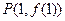 处的切线方程为
处的切线方程为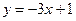 。若函数
。若函数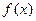 在
在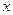 =-2处有极值,求
=-2处有极值,求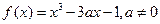 .
.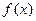 的单调区间;
的单调区间; 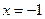 处取得极值,直线
处取得极值,直线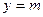 与
与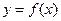 的图象有三个不同的交点,求
的图象有三个不同的交点,求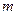 的取值范围。
的取值范围。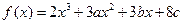 在
在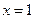 及
及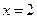 时取得极值.
时取得极值.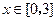 ,都有
,都有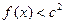 成立,求c的取值范围.
成立,求c的取值范围.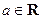 ,若函数
,若函数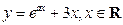 有大于零的极值点,则
有大于零的极值点,则



 已知函数
已知函数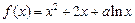 .
.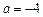 ,求函数
,求函数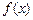 的极值;
的极值;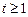 时,不等式
时,不等式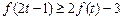 恒成立,求实数
恒成立,求实数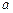 的取值范围.
的取值范围.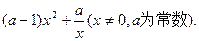
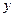 =
= 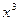 -12
-12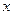 +16在 [-3,3]上的最大值、最小值分别是( )
+16在 [-3,3]上的最大值、最小值分别是( )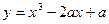 在
在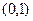 内有极小值,则实数
内有极小值,则实数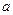 的取值范围为( )
的取值范围为( )