题目内容
16．等腰三角形ABC绕底边上的中线AD所在的直线旋转所得的几何体是（ ）| A． | 圆台 | B． | 圆锥 | C． | 圆柱 | D． | 球 |
分析 由AD⊥BC可得旋转后几何体为圆锥．
解答 
解：∵△ABC是等腰三角形，AB=AC，D是BC的中点，
∴AD⊥BC，
∴△ABC绕AD旋转后所得几何体为以BC为底面直径，以DA为高的圆锥，
故选：B．
点评 本题考查了圆锥的定义，属于基础题．
练习册系列答案
相关题目
7．已知函数f（x）=（2cos2x-1）sin2x+$\frac{1}{2}$cos4x，若α∈（$\frac{π}{2}$，π）且f（α）=$\frac{{\sqrt{2}}}{2}$，则α的值是（ ）
| A． | $\frac{5π}{8}$ | B． | $\frac{11π}{16}$ | C． | $\frac{9π}{16}$ | D． | $\frac{7π}{8}$ |
4．
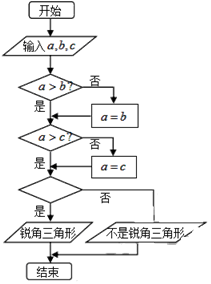如图程序框图中，若输入互不相等的三个正实数a，b，c，要求判断△ABC的形状，则空白的判断框中应填入（ ）
如图程序框图中，若输入互不相等的三个正实数a，b，c，要求判断△ABC的形状，则空白的判断框中应填入（ ）| A． | a2+b2＞c2？ | B． | a2+c2＞b2？ | C． | b2+c2＞a2？ | D． | b2+a2=c2？ |
11．设随机变量X～N（100，σ），p（80＜X≤120）=$\frac{3}{4}$，则p（X＞120）=（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
1．设等差数列{an}的前n项为Sn，已知S13＞0，S14＜0，若ak•ak+1＜0，则k=（ ）
| A． | 6 | B． | 7 | C． | 13 | D． | 14 |
8．若直线过点（1，2），（4，2+$\sqrt{3}$）则此直线的倾斜角是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |