题目内容
设a，b是异面直线，下列命题正确的是（ ）
| A、过不在a、b上的一点P一定可以作一条直线和a、b都相交 |
| B、过不在a、b上的一点P一定可以作一个平面和a、b都垂直 |
| C、过a一定可以作一个平面与b垂直 |
| D、过a一定可以作一个平面与b平行 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：利用空间中线线、线面、面面间的位置关系求解．
解答：
解：A不正确，若点P和直线a确定平面α，
当b∥α时，满足条件的直线不存在．
B不正确，若存在，则有a∥b，这与a、b是异面直线矛盾．
C不正确，只有a、b垂直时才能作出满足条件的平面．
只有D正确，过a一定可以作一个平面与b平行．
故选：D．
当b∥α时，满足条件的直线不存在．
B不正确，若存在，则有a∥b，这与a、b是异面直线矛盾．
C不正确，只有a、b垂直时才能作出满足条件的平面．
只有D正确，过a一定可以作一个平面与b平行．
故选：D．
点评：本题考查直线与直线的位置关系的判断，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
已知二次不等式ax2+2x+b＞0的解集为{x|x≠-
}，且a＞b，则
的最小值是（ ）
| 1 |
| a |
| a2+b2 |
| a-b |
A、2
| ||
B、2
| ||
C、3
| ||
D、3
|
如果实数x，y满足条件
，那么2x-y的最大值为（ ）
|
| A、-1 | B、-2 | C、2 | D、1 |
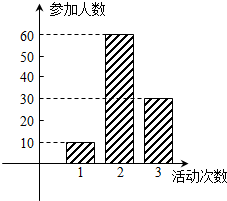某中学号召学生在暑假期间至少参加一次社会公益活动，该校文学社有100名学生，他们参加活动的次数统计如图所示，求：