题目内容
9.已知向量$\overrightarrow{OA}$=(λcosα,λsinα),$\overrightarrow{OB}$=(-sinβ,cosβ),其中O为坐标原点.(1)若λ=-1且β=α-$\frac{π}{6}$,求$\overrightarrow{OA}$•$\overrightarrow{OB}$的值;
(2)若β=α-$\frac{π}{6}$,求向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角;
(3)若|$\overrightarrow{AB}$|≥2|$\overrightarrow{OB}$|对任意实数α、β都成立,求实数λ的取值范围.
分析 (1)先求出向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的坐标,再利用两个向量的数量积公式、两角和差的正弦公式,计算$\overrightarrow{OA}$•$\overrightarrow{OB}$,可得结果.
(2)由(1)可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,计算cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$的值,可得向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角<$\overrightarrow{OA}$,$\overrightarrow{OB}$>的值.
(3)由|$\overrightarrow{AB}$|≥2|$\overrightarrow{OB}$|恒成立,化简可得sin(β-α)≥$\frac{3{-λ}^{2}}{2λ}$恒成立,故有$\frac{3{-λ}^{2}}{2λ}$≤-1,即 $\frac{(λ-3)(λ+1)}{2λ}$≥0,再用穿根法求得λ的范围.
解答 解:(1)∵向量$\overrightarrow{OA}$=(λcosα,λsinα),$\overrightarrow{OB}$=(-sinβ,cosβ),λ=-1且β=α-$\frac{π}{6}$,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=sinβcosα-sinαcosβ=sin(β-α)=sin(-$\frac{π}{6}$)=-sin$\frac{π}{6}$=-$\frac{1}{2}$.
(2)由β=α-$\frac{π}{6}$,$\overrightarrow{OA}$与$\overrightarrow{OB}$=-$\frac{1}{2}$,|$\overrightarrow{OA}$|=1,|$\overrightarrow{OB}$|=1,
可得cos<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=$\frac{-\frac{1}{2}}{1×1}$=-$\frac{1}{2}$,∴向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=120°.
(3)由题意可得,$\overrightarrow{AB}$=(-sinβ-λcosα,cosβ-λsinα),∴|$\overrightarrow{AB}$|=$\sqrt{{(-sinβ-λcosα)}^{2}{+(cosβ-λsinα)}^{2}}$,
故由|$\overrightarrow{AB}$|≥2|$\overrightarrow{OB}$|恒成立,可得 $\sqrt{{(-sinβ-λcosα)}^{2}{+(cosβ-λsinα)}^{2}}$≥2,化简可得sin(β-α)≥$\frac{3{-λ}^{2}}{2λ}$恒成立,
故有$\frac{3{-λ}^{2}}{2λ}$≤-1,即 $\frac{(λ-3)(λ+1)}{2λ}$≥0,用穿根法求得-1≤λ<0或λ≥3.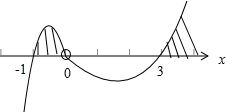
点评 本题主要考查两个向量的数量积的定义,两角和差的正弦公式,两个向量的数量积公式,函数的恒成立问题,以及分式不等式的解法,属于中档题.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
| A. | 32 | B. | 18 | C. | 16 | D. | 10 |
| A. | 定义在(a,b)上的函数f(x),若存在x1<x2时,有f(x1)<f(x2),那么f(x)在(a,b)上为增函数 | |
| B. | 定义在(a,b)上的函数f(x),若有无穷多对x1,x2∈(a,b)使得x1<x2时,有f(x1)<f(x2),那么f(x)在(a,b)上为增函数 | |
| C. | 若f(x)在区间I1上为增函数,在区间I2上也为增函数,那么f(x)在I1∪I2上也一定为增函数 | |
| D. | 若f(x)在区间I上为增函数,且f(x1)<f(x2),(x1,x2∈I),那么x1<x2 |
| A. | $\frac{1}{2}$ | B. | 1 | C. | $-\frac{1}{2}$ | D. | -1 |