题目内容
【题目】在极坐标系下,方程![]() 的图形为如图所示的“幸运四叶草”,又称为玫瑰线.
的图形为如图所示的“幸运四叶草”,又称为玫瑰线.

(1)当玫瑰线的![]() 时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
时,求以极点为圆心的单位圆与玫瑰线的交点的极坐标;
(2)求曲线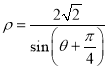 上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
上的点M与玫瑰线上的点N距离的最小值及取得最小值时的点M、N的极坐标(不必写详细解题过程).
【答案】(1)![]() 和
和![]() ;(2)最小值为
;(2)最小值为![]() ,M,N的极坐标分别为
,M,N的极坐标分别为![]() ,
,![]()
【解析】
(1)把![]() 与
与![]() 联立,解方程组即得以极点为圆心的单位圆与玫瑰线的交点的极坐标;(2)曲线
联立,解方程组即得以极点为圆心的单位圆与玫瑰线的交点的极坐标;(2)曲线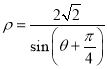 的直角坐标方程为
的直角坐标方程为![]() 再利用数形结合求出点M、N的极坐标.
再利用数形结合求出点M、N的极坐标.
(1)以极点为圆心的单位圆为![]() 与
与![]() 联立,得
联立,得![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() 或
或![]() ,
,
从而得到以极点为圆心的单位圆与玫瑰线的交点的极坐标为![]() 和
和![]() .
.
(2)曲线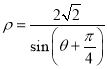 的直角坐标方程为
的直角坐标方程为![]() .
.
玫瑰线![]() 极径的最大值为2,且在点
极径的最大值为2,且在点![]() 取得,
取得,
连接O,![]() 与
与![]() 垂直且交于点
垂直且交于点![]() ,
,
所以点M与点N的距离的最小值为![]() ,
,
此时对应的点M,N的极坐标分别为![]() ,
,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目