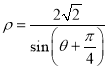题目内容
【题目】设A,B为函数![]() 图象上相异两点,且A,B的横坐标之积为常数
图象上相异两点,且A,B的横坐标之积为常数![]() ,若
,若![]() 在A,B两点处的切线存在交点,则称这个交点为函数
在A,B两点处的切线存在交点,则称这个交点为函数![]() 的“
的“![]() 点”。
点”。
(1)求函数![]() 的“
的“![]() 点”的纵坐标的取值范围;
点”的纵坐标的取值范围;
(2)判断函数![]() 的
的![]() 点”在哪个象限,并说明理由.
点”在哪个象限,并说明理由.
【答案】(1)![]() ,(2)第一象限,理由见解析。
,(2)第一象限,理由见解析。
【解析】
(1)设![]() ,求得导数和切线方程,求得交点的纵坐标,结合基本不等式可得所求范围;
,求得导数和切线方程,求得交点的纵坐标,结合基本不等式可得所求范围;
(2)设![]() ,求得导数,以及切线方程,求交点,由构造函数法,即可得到交点的坐标均为正数.
,求得导数,以及切线方程,求交点,由构造函数法,即可得到交点的坐标均为正数.
解:(1)设![]() ,
,
以A,B为切点的切线方程为![]() ,消去x得
,消去x得

所以函数![]() 的“
的“![]() 点”的纵坐标的取值范围为
点”的纵坐标的取值范围为![]()
(2)设![]() ,
,![]() ,
,
以A,B为切点的切线方程为![]() ,
, ![]() ,
,
令![]() ,可得
,可得 ,
,
设![]() ,可令
,可令![]() ,
,
![]() ,即
,即![]() 递增,
递增,
![]() ,即
,即![]() ,
,
又 ,则
,则 ,
,
函数![]() 的
的![]() 点的横坐标和纵坐标均为正数,一定落在第一象限。
点的横坐标和纵坐标均为正数,一定落在第一象限。

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目