题目内容
16.设集合P={x|0≤x≤4},Q={y|0≤y≤4},能表示集合P到集合Q的函数关系的有( )
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
分析 根据函数的定义,在集合P中的任一元素在集合Q中都要有唯一的一个元素和它对应,进而可以得到答案.
解答 解:由函数的定义知①中的定义域不是P,④中集合P中有的元素在集合Q中对应两个函数值不符合函数定义,故不对,
只有②③成立.
故选C.
点评 本题主要考查函数的定义的问题.集合P到集合Q的函数关系一定要满足:对集合P中任一元素根据对应关系都要在集合Q中找到对应函数值.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
14.记函数f(x)($\frac{1}{e}$<x≤e,e=2.71828…是自然对数的底数)的导数为f′(x),函数g(x)=(x-$\frac{1}{\sqrt{e}}$)f′(x)只有一个零点,且g(x)的图象不经过第一象限,当x>$\frac{1}{e}$时,f(x)+4lnx+$\frac{1}{lnx+1}$>$\frac{1}{\sqrt{e}}$,f[f(x)+4lnx+$\frac{1}{lnx+1}$]=0,下列关于f(x)的结论,成立的是( )
| A. | 当x=e时,f(x)取得最小值 | B. | f(x)最大值为1 | ||
| C. | 不等式f(x)<0的解集是(1,e) | D. | 当$\frac{1}{e}$<x<1时,f(x)>0 |
15.若a=2${\;}^{\frac{1}{3}}$,b=ln2,c=log5sin$\frac{4π}{5}$,则( )
| A. | c>a>b | B. | b>a>c | C. | a>b>c | D. | b>c>a |
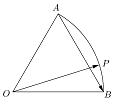 如图,已知半径为1的扇形AOB,∠AOB=60°,P为弧$\widehat{AB}$上的一个动点,则$\overrightarrow{OP}•\overrightarrow{AB}$取值范围是[$-\frac{1}{2}$,$\frac{1}{2}$].
如图,已知半径为1的扇形AOB,∠AOB=60°,P为弧$\widehat{AB}$上的一个动点,则$\overrightarrow{OP}•\overrightarrow{AB}$取值范围是[$-\frac{1}{2}$,$\frac{1}{2}$].