题目内容
1.设集合A={x|-1≤x≤2},B={x|m-1≤x≤2m+1},已知B⊆A.(1)当x∈N时,求集合A的子集的个数;
(2)求实数m的取值范围.
分析 (1)利用列举法得到集合A的元素,然后求其子集;
(2)分类讨论:讨论集合B为空集和非空时,利用B⊆A,确定m的取值范围即可.
解答 解:(1)∵当x∈N时,A={0,1,2},∴集合A的子集的个数为23=8.
(2)①当m-1>2m+1,即m<-2时,B=∅,符合题意;
②当m-1≤2m+1,即m≥-2时,B≠∅.由B⊆A,借助数轴,如图所示,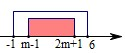
得$\left\{{\begin{array}{l}{m-1≥-1}\\{2m+1≤2}\end{array}}\right.$解得0≤m≤$\frac{1}{2}$,所以0≤m≤$\frac{1}{2}$.
综合①②可知,实数m的取值范围为$\{m|m<-2或0≤m≤\frac{1}{2}\}$.
点评 本题主要考查集合关系的应用,注意要对集合B进行分类讨论.

练习册系列答案
相关题目
11.设全集U=Z,集合A={x|1≤x<7,x∈Z},B={x=2k-1,k∈Z},则A∩(∁UB)=( )
| A. | {1,2,3,4,5,6} | B. | {1,3,5} | C. | {2,4,6} | D. | ∅ |
16.设集合P={x|0≤x≤4},Q={y|0≤y≤4},能表示集合P到集合Q的函数关系的有( )


| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
2.不等式|x2-2|<2的解集是( )
| A. | (-2,0)∪(0,2) | B. | (-2,2) | C. | (-1,0)∪(0,1) | D. | (-1,1) |
19.下列有关命题的说法正确的是( )
| A. | 命题:若x=y,则sinx=siny的逆否命题为真命题 | |
| B. | x>2是x2-3x+2>0的必要不充分条件 | |
| C. | 命题:若x2=1,则x=1的否命题为“若x2=1,则x≠1” | |
| D. | 命题:?x∈R使得x2+x+1<0的否定为:?x∈R均有x2+x+1<0 |
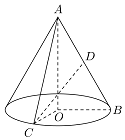 如图,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以
如图,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以