题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+1,x≤0}\\{-2x,x>0}\end{array}\right.$,(1)画出函数的图象并求其单调性;
(2)若方程f(x)=a无实根,求实数a的范围.
分析 (1)画出分段函数的图象,由图象可得单调区间;
(2)若方程f(x)=a无实根,即为y=a与函数f(x)的图象无交点,通过图象观察即可得到a的范围.
解答 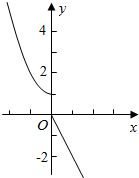 解:(1)f(x)的图象如右所示:
解:(1)f(x)的图象如右所示:
由图象可得f(x)在(-∞,0],(0,+∞)
为减函数;
(2)由图象可得,
若方程f(x)=a无实根,
即为y=a与函数f(x)的图象无交点,
则有0≤a<1.
故a的范围是[0,1).
点评 本题考查分段函数的图象及应用:求单调性和方程的解,考查数形结合的思想方法,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
3.已知等差数列{an}满足a2=2,a6=0,则数列{an}的公差为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
20.经过圆x2-2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是( )
| A. | x-y+1=0 | B. | x-y-1=0 | C. | x+y-1=0 | D. | x+y+1=0 |
1.已知点(a,b)与点(2,0)位于直线2x+3y-1=0的同侧,且a>0,b>0,则z=$\frac{4b+1}{4a-1}$的取值范围是( )
| A. | (-$\frac{7}{3}$,1) | B. | ($-∞,-\frac{7}{3}$)∪(1,+∞) | C. | ($-∞,-\frac{7}{3}$)∪(0,+∞) | D. | ($-\frac{7}{3}$,0) |
2.小明在玩投石子游戏,第一次走1米放1颗石子,第二次走2米放2颗石子…第n次走n米放2n-1颗石子,当小明一共走了55米时,他投放石子的总数是( )
| A. | 36 | B. | 254 | C. | 1023 | D. | 512 |
 已知函数f(x)=|x|(x-2).
已知函数f(x)=|x|(x-2).