题目内容

17．已知函数f（x）=|x|（x-2）．
（1）画出函数的图象；
（2）利用图象回答：当k为何值时，方程|x|（x-2）=k有一个解？有两个解？有三个解？

分析 （1）作函数f（x）=|x|（x-2）的图象即可，
（2）结合图象，将方程的解化为函数的图象的交点，从而确定解的个数．

解答 解：（1）作函数f（x）=|x|（x-2）的图象如下，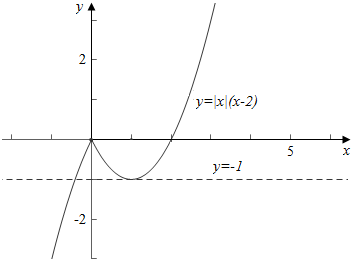
，
（2）结合图象可知，
当k＞0或k＜-1时，方程|x|（x-2）=k有一个解，
当k=0或k=-1时，方程|x|（x-2）=k有两个解，
当-1＜k＜0时，方程|x|（x-2）=k有三个解．

点评 本题考查了学生的作图能力与数形结合的思想的应用．

练习册系列答案
相关题目
7．已知P={a，b，c}，Q={-1，0，1，2}，f是从P到Q的映射，则满足f（a）=0的映射的个数为（　　）
A．8B．9C．16D．81
8．在△ABC中，内角A，B，C的对边分别为a，b，c，且a，b，c成公差为1的等差数列，C=2A．
（1）求a，b，c的值；
（2）求$\overrightarrow{AC}在\overrightarrow{CB}$方向上的投影．
5．已知集合A={x∈Z|-3≤x-1≤1}，B={1，2，3}，C={3，4，5，6}．
（1）求A的非空真子集的个数；
（2）求B∪C，A∪（B∩C）．
12．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x≤0}\\{-2x，x＞0}\end{array}\right.$，
（1）画出函数的图象并求其单调性；
（2）若方程f（x）=a无实根，求实数a的范围．
2．已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）-g（x）=x3+x2+1，则f（2）+g（2）=（　　）
A．13B．-3C．-13D．3
9．已知函数f（x）对任意实数x、y都有f（x+y）=f（x）+f（y），且x＞0时，f（x）＞0．
（1）证明：f（x）是奇函数；
（2）证明：f（x）在（-∞，+∞）内是增函数；
（3）若f（2x）＞f（x+3），试求x的取值范围．
6．已知某三角形的面积为S，证明：用斜二测画法得到的其直观图的面积为S′=$\frac{\sqrt{2}}{4}$S．
7．计算：log2$\frac{1}{25}$•log3$\frac{1}{8}$•log5$\frac{1}{9}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网