题目内容
11.如图1,已知四边形BCDE为直角梯形,∠B=90°,BE∥CD,且BE=2CD=2BC=2,A为BE的中点.将△EDA沿AD折到△PDA位置(如图2),连结PC,PB构成一个四棱锥P-ABCD.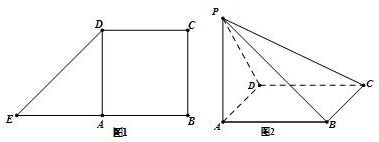
(Ⅰ)求证AD⊥PB;
(Ⅱ)若PA⊥平面ABCD,求点C到平面PBD的距离.
分析 (Ⅰ)推导出ABCD为平行四边形,AD∥BC,AD⊥BE,AD⊥AB,AD⊥PA,从而AD⊥平面PAB,由此能证明AD⊥PB.
(Ⅱ)利用等体积方法,求点C到平面PBD的距离.
解答 (Ⅰ)证明:在图1中,因为AB∥CD,AB=CD,
所以ABCD为平行四边形,所以AD∥BC,
因为∠B=90°,所以AD⊥BE,
当三角形EDA沿AD折起时,AD⊥AB,AD⊥AE,
即:AD⊥AB,AD⊥PA,
又AB∩PA=A,所以AD⊥平面PAB,
又因为PB?平面PAB,所以AD⊥PB.---------------------------------------------------(6分)
(Ⅱ)解:PA⊥平面ABCD,${S_{△BCD}}=\frac{1}{2}$,
∵$PD=BD=PB=\sqrt{2}$,∴${S_{△PBD}}=\frac{{\sqrt{3}}}{2}$,
∵PA=1,设点C到平面PBD的距离为h
∴VC-PBD=VP-BCD,∴$\frac{1}{3}•\frac{{\sqrt{3}}}{2}•h=\frac{1}{3}•\frac{1}{2}•1$,∴$h=\frac{{\sqrt{3}}}{3}$
答:点C到平面PBD的距离为$\frac{{\sqrt{3}}}{3}$.------------------------------------(12分)
点评 本题考查异面直线垂直的证明,考查点C到平面PBD的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.“k>4”是“方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
20.若复数Z满足Z•i=1+i(i是虚数单位),则Z的共轭复数是( )
| A. | 1+i | B. | -1-i | C. | -1+i | D. | 1-i |