题目内容
19.已知二项式($\sqrt{x}$+$\frac{1}{2\root{4}{x}}$)n的展开式中所有奇数项的二项式系数之和为512,求二项式($\sqrt{x}$+$\frac{1}{2\root{4}{x}}$)n的展开式的所有有理项.分析 二项式($\sqrt{x}$+$\frac{1}{2\root{4}{x}}$)n的展开式中所有奇数项的二项式系数之和为512,可得$\frac{1}{2}×{2}^{n}$=512,解得n.再利用通项公式即可得出.
解答 解:∵二项式($\sqrt{x}$+$\frac{1}{2\root{4}{x}}$)n的展开式中所有奇数项的二项式系数之和为512,
∴$\frac{1}{2}×{2}^{n}$=512,解得n=10.
∴$(\sqrt{x}+\frac{1}{2\root{4}{x}})^{10}$的通项公式:Tr+1=${∁}_{10}^{r}$$(\sqrt{x})^{10-r}$$(\frac{1}{2\root{4}{x}})^{r}$=2-r${∁}_{10}^{r}$${x}^{5-\frac{3r}{4}}$.(r=0,1,2,…,10).
∵5-$\frac{3r}{4}$∈Z,∴r=0,4,8,
∴所有有理项为T1=${∁}_{10}^{0}×{2}^{0}×{x}^{5}$=x5,T5=${∁}_{10}^{4}×{2}^{-4}×{x}^{2}$=$\frac{105}{8}{x}^{2}$,T9=${∁}_{10}^{8}$×2-8×x-1=$\frac{45}{256x}$.
点评 本题考查了二项式定理的性质及其应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知函数h(x)=ax2+bx+c(a≠0)在区间(a,c)上为偶函数,则h(-1)=( )
| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
14.某中学从4名男生和3名女生中推荐3人参加社会公益活动,若选出的3人中既有男生又有女生,则不同的选法共有( )
| A. | 90种 | B. | 60种 | C. | 35种 | D. | 30种 |
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
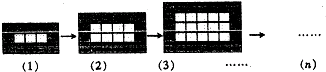

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
9.若函数f(x)=2x2+(x-2a)|x-a|在区间[-3,1]上不是单调函数,则实数a的取值范围是( )
| A. | [-4,1] | B. | [-3,1] | C. | (-6,2) | D. | (-6,1) |