题目内容
16.“k>4”是“方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
分析 求出方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆的k的范围,结合集合的包含关系判断即可.
解答 解:∵方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆,
∴$\left\{\begin{array}{l}{9-k>0}\\{k-4>0}\\{9-k≠k-4}\end{array}\right.$,解得:4<k<9且k≠$\frac{13}{2}$,
故k>4”是“方程$\frac{{x}^{2}}{9-k}$+$\frac{{y}^{2}}{k-4}$=1表示的图形为椭圆”的必要不充分条件,
故选:B.
点评 本题考查了充分必要条件,考查椭圆的方程,是一道基础题.

练习册系列答案
相关题目
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
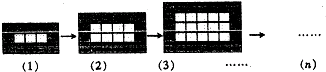

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
5.设正数数列{an}的前n项和为bn,数列{bn}的前n项之积为cn,且bn+cn=1,则数列{$\sqrt{\frac{1}{{a}_{n}}}$}的前n项和Sn中大于2016的最小项为第63项.
6.集合A={-2,-1,0,1,3},集合B={x|x>$\frac{1}{2}$ },则集合A∩(∁RB ) 等于( )
| A. | {1,3} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {0,1,3} |