题目内容
对于函数y=f(x)的定义域为D,如果存在区间[m,n]⊆D同时满足下列条件:①f(x)在[m,n]是单调的;②当定义域为[m,n]时,f(x)的值域也是[m,n],则称区间[m,n]是该函数的“H区间”.若函数f(x)=
存在“H区间”,则正数a的取值范围是( )
|
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
考点:分段函数的应用
专题:函数的性质及应用
分析:根据定义,利用分段函数结合函数的图象函数的最值求出a的范围即可.
解答:
解:当x>0时,f(x)=alnx-x,
f′(x)=
-1=
,
由f′(x)≥0,
得
≥0,得0<x≤a,此时函数f(x)为增函数,
当x=n时,取得最大值,
当x=m时,取最小值,
即
,
即方程alnx-x=x有两个解,
即方程a=
有两个解,作出y=
的图象,
由图象以及函数的导数可知,
当x>1时,y=
,在x=e处取得最小值2e,
在x=a时,y=
,
故方程a=
有两个解,
∴a≤
,
解得a≤e2,正数a的取值范围是(2e,e2].
当x>a时,函数f(x)为单调减函数,
则当x=m时,取得最大值,
当x=n时,取得最小值,
即
,
两式相减可得,alnm-alnn=0,即m=n,不符合;
当x≤0时,函数f(x)为减函数,
则当x=m时取最大值,
当x=n时,取得最小值,
即
,两式相减,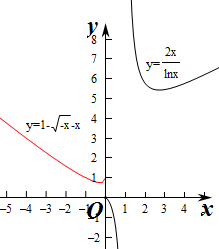
可以得到
+
=1,回代到方程组的第一个式子得到
1-
-a=n,
整理得到1-
-n=a,
由图象可知,方程有两个解,
则
<a≤1,
综上正数a的取值范围是(
,1]∪(2e,e2],
故选:B
f′(x)=
| a |
| x |
| a-x |
| x |
由f′(x)≥0,
得
| a-x |
| x |
当x=n时,取得最大值,
当x=m时,取最小值,
即
|
即方程alnx-x=x有两个解,
即方程a=
| 2x |
| lnx |
| 2x |
| lnx |
由图象以及函数的导数可知,
当x>1时,y=
| 2x |
| lnx |
在x=a时,y=
| 2a |
| lna |
故方程a=
| 2x |
| lnx |
∴a≤
| 2a |
| lna |
解得a≤e2,正数a的取值范围是(2e,e2].
当x>a时,函数f(x)为单调减函数,
则当x=m时,取得最大值,
当x=n时,取得最小值,
即
|
两式相减可得,alnm-alnn=0,即m=n,不符合;
当x≤0时,函数f(x)为减函数,
则当x=m时取最大值,
当x=n时,取得最小值,
即
|
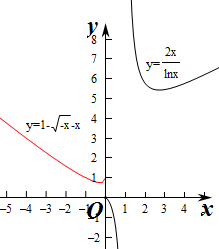
可以得到
| -m |
| -n |
1-
| -n |
整理得到1-
| -n |
由图象可知,方程有两个解,
则
| 3 |
| 4 |
综上正数a的取值范围是(
| 3 |
| 4 |
故选:B
点评:本题主要考查函数单调性的应用以及函数的最值考查数形结合,综合性较强.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
甲、乙、丙三人站到共有7级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法种数是( )
| A、258 | B、306 |
| C、336 | D、296 |
在平面直角坐标系中,不等式
(a为常数)表示平面区域的面积为9,则
的最小值为( )
|
| y-2 |
| x+4 |
| A、-1 | ||
B、
| ||
C、
| ||
D、-
|
若两条平行线l1,l2的方程分别是2x+3my-m+2=0,mx+6y-4=0,记l1,l2之间的距离为d,则m,d分别为( )
A、m=2,d=
| ||||
B、m=2,d=
| ||||
C、m=2,d=
| ||||
D、m=-2,d=
|