题目内容
已知直线L1:y=kx和L2:y=-
,分别与抛物线W:y2=2x和抛物线M:y2=4x交于A,B,C,D四点,则
= .
| 2x |
| k |
| S△OAC |
| S△OBD |
考点:曲线与方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:联立直线方程和抛物线方程,求得交点A,B,C,D,再由三角形的面积公式,即可求得.
解答:
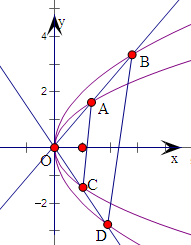 解:由
解:由
解得交点A(
,
),由
解得交点B(
,
),
由
解得交点C(
k2,-k),由
解得交点D(k2,-2k),
则S△OAC=
|OA|•|OC|sin∠AOC=
•
sin∠AOC,
S△OBD=
|OB|•|OD|sin∠AOC=
•
sin∠AOC,
则有
=
=
.
故答案为:
.
 解:由
解:由
|
| 2 |
| k2 |
| 2 |
| k |
|
| 4 |
| k2 |
| 4 |
| k |
由
|
| 1 |
| 2 |
|
则S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
4(
|
|
S△OBD=
| 1 |
| 2 |
| 1 |
| 2 |
16(
|
| k4+4k2 |
则有
| S△OAC |
| S△OBD |
2×
| ||
| 4×1 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查抛物线方程和直线方程联立求交点,考查三角形的面积公式的运用,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
(x≠2)的反函数y=f-1(x)的一个单调减区间是( )
| 1+3x |
| x-2 |
| A、(-2,+∞) |
| B、(2,+∞) |
| C、(3,+∞) |
| D、(-3,+∞) |
已知全集U=R,集合A={x|2x>1},B={x|
>0},则A∩(∁UB)=( )
| 1 |
| x-1 |
| A、{x|x>1} |
| B、{x|0<x<1} |
| C、{x|0<x≤1} |
| D、{x|x≤1} |
若变量x,y满足约束条件
,则目标函数z=3x+y的最大值为( )
|
| A、-4 | B、0 | C、4 | D、8 |
若a,b,c成等比数列,则函数y=ax2+bx+
的图象与x轴交点个数是( )
| c |
| 4 |
| A、0 | B、1 | C、2 | D、0或2 |
 如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
 如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k
如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k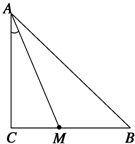 已知等腰Rt△ABC中,∠C=90°.
已知等腰Rt△ABC中,∠C=90°.