题目内容
已知函数f(x)=cos(2x+φ)(0≤φ<π)是奇函数,则f(x)在[0,
]上的最大值与最小值的和为 .
| 3π |
| 4 |
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:根据f(x)是奇函数得到φ=
,利用三角函数的图象和性质即可得到结论.
| π |
| 2 |
解答:
解:∵函数f(x)=cos(2x+φ)(0≤φ<π)是奇函数,
∴φ=
,即函数f(x)=cos(2x+
)=-sin2x,
∵x∈[0,
],∴2x∈[0,
],
即当2x=
时,f(x)取得最小值-1,当2x=
时,函数f(x)取得最大值1,
∴f(x)在[0,
]上的最大值与最小值的和1-1=0,
故答案为:0
∴φ=
| π |
| 2 |
| π |
| 2 |
∵x∈[0,
| 3π |
| 4 |
| 3π |
| 2 |
即当2x=
| π |
| 2 |
| 3π |
| 2 |
∴f(x)在[0,
| 3π |
| 4 |
故答案为:0
点评:本题主要考查三角函数的奇偶性和最值的求解,根据条件求出φ的值是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若方程mx2+(m-4)y2=1表示双曲线,则m的取值范围为( )
| A、0<m<4 | B、m>0 |
| C、m<4 | D、m>4 |
已知F1,F2为平面内两个定点,那么“|MF1|+|MF2|等于常数”是“点M的轨迹是以F1,F2为焦点的椭圆”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
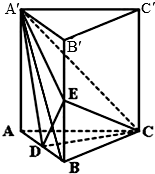 如图,直三棱柱ABC-A′B′C′中,AC=BC=5,AA′=AB=6,D、E分别为AB和BB′上的点,且
如图,直三棱柱ABC-A′B′C′中,AC=BC=5,AA′=AB=6,D、E分别为AB和BB′上的点,且