题目内容
1.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{7}}{4}$,则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率为( )| A. | $\frac{5}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{4}$ |
分析 利用椭圆与双曲线的离心率计算公式即可得出.
解答 解:∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{7}}{4}$,
∴$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{7}}{4}$,解得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{9}{16}$.
则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{9}{16}}$=$\frac{5}{4}$.
故选:A.
点评 本题考查了椭圆与双曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13.过点A(4,a)和B(5,b)的直线与直线y=2x+m平行,则|AB|=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 5 | D. | $\sqrt{5}$ |
10.已知O为坐标原点,F是椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点,A、B分别为椭圆C的左、右顶点,P为椭圆C上一点,且PF⊥x轴.过顶点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB=$\frac{1}{2}$,AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB=$\frac{1}{2}$,AB=1,M是PB的中点.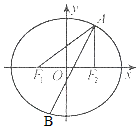 椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$.
椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=$\frac{1}{2}$.