题目内容
求不等式|x-2|-|x-1|＞0的解集．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由不等式|x-2|-|x-1|＞0?不等式|x-2|＞|x-1|?（x-2）2＞（x-1）2即可求得答案．
解答：
解：∵|x-2|-|x-1|＞0，
∴|x-2|＞|x-1|≥0，
∴（x-2）2＞（x-1）2，
可得-4x+4＞-2x+1
∴x＜
．
∴不等式|x-2|-|x-1|＞0的解集为{x|x＜
}．
故答案为：{x|x＜
}．
∴|x-2|＞|x-1|≥0，
∴（x-2）2＞（x-1）2，
可得-4x+4＞-2x+1
∴x＜
| 3 |
| 2 |
∴不等式|x-2|-|x-1|＞0的解集为{x|x＜
| 3 |
| 2 |
故答案为：{x|x＜
| 3 |
| 2 |
点评：本题考查绝对值不等式的解法，将绝对值不等式转化为二次不等式是关键，着重考查转化思想与运算能力，属于中档题．
练习册系列答案
相关题目
若直线y=x+b与曲线y=
有两个交点，则实数b的取值范围是（ ）
| 4-x2 |
A、（2，2
| ||||
B、[2，2
| ||||
C、（-2，2
| ||||
D、（-2
|
下列类比中：
①与圆心距离相等的两弦相等：类比到空间：与球心距离相等的两个数面圆的面积相等；
②圆的面积S=πr2，类比到空间：球的体积为V=πr2；
③圆心与弦（垂直经）中点的连线垂直于弦，类比到空间，球心与截面圆（不经过球心的小截面圆）圆心的连线垂直与截图，
其中正确的类比是（ ）
①与圆心距离相等的两弦相等：类比到空间：与球心距离相等的两个数面圆的面积相等；
②圆的面积S=πr2，类比到空间：球的体积为V=πr2；
③圆心与弦（垂直经）中点的连线垂直于弦，类比到空间，球心与截面圆（不经过球心的小截面圆）圆心的连线垂直与截图，
其中正确的类比是（ ）
| A、①② | B、①③ | C、②③ | D、①②③ |
下面是2×2列联表：
则a+b+c等于（ ）
| y1 | y2 | 总计 | |
| x1 | a | b | 73 |
| x2 | 22 | c | 47 |
| 总计 | 74 | 46 | 120 |
| A、96 | B、97 | C、99 | D、98 |
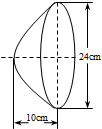如图所示，汽车前灯反光镜与轴截面的交线是抛物线的一部分，灯口所在的圆面与反光镜的轴垂直，灯泡位于抛物线的焦点处．已知灯口的直径是24cm，灯深10cm，那么灯泡与反光镜的顶点（即截得抛物线的顶点）距离为（ ）| A、10cm | B、7.2cm |
| C、3.6cm | D、2.4cm |
已知f（x）=ex（sinx-cosx）（0≤x≤2015π），求则函数f（x）的各极大值之和为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
某同学设计的算法流程图用以计算和式12+22+32+…+20152的值，则在判断框中应填写（ ）
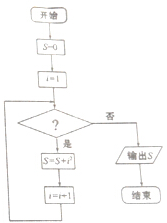
| A、i≤2015 |
| B、i≤2016 |
| C、≥2015 |
| D、i≥2016 |