题目内容
17.对于函数f(x),在使f(x)≥M成立的所有常数M中,我们把M的最大值称为f(x)的“下确界”,则函数f(x)=1-4x+$\frac{1}{5-4x}$,x∈(-∞,$\frac{5}{4}$)的“下确界“等于( )| A. | -2 | B. | -4 | C. | -8 | D. | 不能确定 |
分析 由基本不等式可得f(x)的最小值为-2,可得M≤-2,再由“下确界“的定义,即可得到.
解答 解:函数f(x)=1-4x+$\frac{1}{5-4x}$,
由x∈(-∞,$\frac{5}{4}$),可得5-4x>0,
即有f(x)=(5-4x)+$\frac{1}{5-4x}$-4≥2$\sqrt{(5-4x)•\frac{1}{5-4x}}$-4
=2-4=-2.
当且仅当5-4x=1,可得x=1,取得等号.
即有M≤-2,
则函数f(x)的“下确界“等于-2.
故选:A.
点评 本题考查新定义的理解和运用,考查基本不等式的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.“a+b是偶数”是“a、b都是偶数”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 非充分非必要条件 |
5.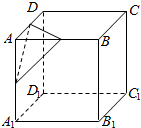 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )| A. | 此多面体的表面积为$\frac{47}{8}$a2 | B. | 体对角线AC1垂直于截面 | ||
| C. | 截面平行于平面CB1D1 | D. | 有10个顶点 |
7.如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{2016}$的值的一个程序框图,则判断框内应填入的条件是( )
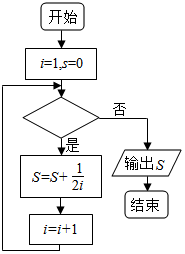

| A. | i≤1007 | B. | i≤1008 | C. | i>1008 | D. | i>1007 |
 某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下:
某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下: