题目内容
已知数列{an}是首项为a1，公差为d（0＜d＜2π）的等差数列，若数列{cosan}是等比数列，则其公比为 ．
考点：等差数列与等比数列的综合
专题：等差数列与等比数列
分析：根据等比数列的定义得
=
，根据等差数列的通项公式化简，再由积化和差和和差化积化简得出sind=0，由公差的范围求得公差d，再求出公比q的值．
| cosan+1 |
| cosan |
| cosa2 |
| cosa1 |
解答：
解：∵数列{an}是首项为a1，公差为d（0＜d＜2π）的等差数列，
∴an=a1+（n-1）d，
∵数列{cosan}是等比数列，
∴
=
，即
=
①，
∴2cosa1cos（a1+nd）=2cos（a1+d）cos[a1+（n-1）d]，
积化和差得cos（2a1+nd）+cosnd=cos（2a1+nd）+cos（n-2）d，
∴cos（n-2）d-cosnd=0，
和差化积得2sin[（n-1）d]sind=0，对任意的正整数n都成立，
∴sind=0，0＜d＜2π，则d=π．
由①得，公比q=-1．
故答案为：-1．
∴an=a1+（n-1）d，
∵数列{cosan}是等比数列，
∴
| cosan+1 |
| cosan |
| cosa2 |
| cosa1 |
| cos(a1+nd) |
| cos[a1+(n-1)d] |
| cos(a1+d) |
| cosa1 |
∴2cosa1cos（a1+nd）=2cos（a1+d）cos[a1+（n-1）d]，
积化和差得cos（2a1+nd）+cosnd=cos（2a1+nd）+cos（n-2）d，
∴cos（n-2）d-cosnd=0，
和差化积得2sin[（n-1）d]sind=0，对任意的正整数n都成立，
∴sind=0，0＜d＜2π，则d=π．
由①得，公比q=-1．
故答案为：-1．
点评：本题考查等比数列的公比的求法，等差数列的通项公式，解题时要认真审题，注意积化和差公式与和差化积公式的灵活运用，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
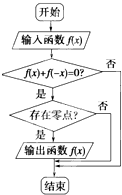某程序框图如图所示，现输入四个函数（1）f（x）=x2，（2）f（x）=