题目内容
经调查统计,某种型号的汽车在匀速行驶中,每小时的耗油量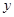 (升)关于行驶速度
(升)关于行驶速度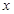 (千米/时)的函数可表示为
(千米/时)的函数可表示为 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为
千米/时的条件下,该种型号的汽车从甲地 到乙地的耗油量记为 (升).
(升).
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)讨论函数 的单调性,当
的单调性,当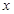 为多少时,耗油量
为多少时,耗油量 为最少?最少为多少升?
为最少?最少为多少升?
(Ⅰ)
 ;(Ⅱ)当
;(Ⅱ)当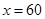 ,从甲地到乙地的耗油量
,从甲地到乙地的耗油量 最少,最少耗油量为7升.
最少,最少耗油量为7升.
解析试题分析:(Ⅰ)由题意得,汽车从甲地到乙地行驶了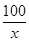 小时,又因为每小时的耗油量
小时,又因为每小时的耗油量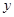 (升)关于行驶速度
(升)关于行驶速度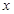 (千米/时)的函数可表示为
(千米/时)的函数可表示为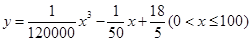 ,二者相乘即得
,二者相乘即得 .(Ⅱ)由(Ⅰ)有,
.(Ⅱ)由(Ⅰ)有,
 ,利用导数可得其最小值.
,利用导数可得其最小值.
试题解析:(Ⅰ)由题意得,汽车从甲地到乙地行驶了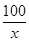 小时, (2分)
小时, (2分)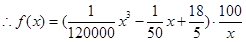
 . (5分)
. (5分)
(Ⅱ)由(Ⅰ)有,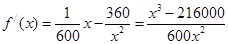 . (8分)
. (8分)
令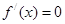 ,得
,得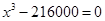 ,
,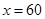 . (9分)
. (9分)
①当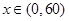 时,
时,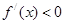 ,
, 是减函数; (10分)
是减函数; (10分)
②当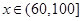 时,
时,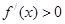 ,
, 是增函数; (11分)
是增函数; (11分)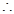 当
当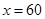 ,即汽车的行驶速度为
,即汽车的行驶速度为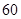 (千米/时)时,从甲地到乙地的耗油量
(千米/时)时,从甲地到乙地的耗油量 为最少,最少耗油量为
为最少,最少耗油量为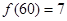 (升). (12分)
(升). (12分)
考点:函数及导数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
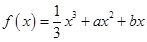
 .
. 经过点
经过点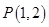 ,曲线
,曲线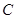 在点
在点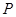 处的切线与直线
处的切线与直线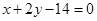 垂直,求
垂直,求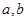 的值;
的值;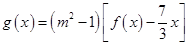 (
(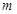 为实常数,
为实常数, )的极大值与极小值之差;
)的极大值与极小值之差; 在区间
在区间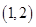 内存在两个不同的极值点,求证:
内存在两个不同的极值点,求证: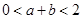 .
.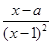 ,x∈(1,+∞).
,x∈(1,+∞).
 时,求
时,求 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.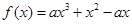 ,其中
,其中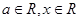 .
. 时,求函数
时,求函数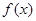 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围;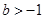 ,如果存在
,如果存在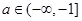 ,使得函数
,使得函数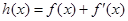
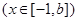 在
在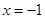 处取得最小值,试求
处取得最小值,试求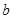 的最大值.
的最大值.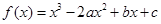 .
.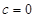 时,
时,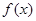 的图象在点
的图象在点 处的切线平行于直线
处的切线平行于直线 ,求
,求 的值;
的值;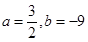 时,
时,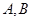 处有极值,
处有极值, 为坐标原点,若
为坐标原点,若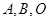 三点共线,求
三点共线,求 的值.
的值.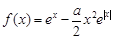 .
.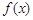 是
是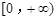 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;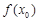 >x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由.
>x0+1成立?如果存在,请求出符合条件的一个x0;如果不存在,请说明理由. ,其中
,其中 是自然对数的底数,
是自然对数的底数,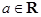 .
. 的单调区间;
的单调区间;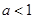 时,试确定函数
时,试确定函数 的零点个数,并说明理由.
的零点个数,并说明理由.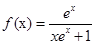 .
.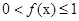 ;
;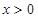 时,
时,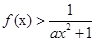 ,求
,求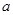 的取值范围.
的取值范围.