题目内容
已知函数 ,其中
,其中 是自然对数的底数,
是自然对数的底数,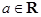 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)当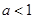 时,试确定函数
时,试确定函数 的零点个数,并说明理由.
的零点个数,并说明理由.
(Ⅰ) 的单调减区间为
的单调减区间为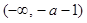 ;单调增区间为
;单调增区间为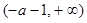 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)求导得,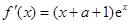 ,因为
,因为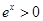 ,所以
,所以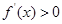 的解集为
的解集为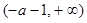 ,即单调递增区间;
,即单调递增区间;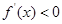 的解集为
的解集为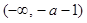 ,即单调递减区间;(Ⅱ)函数
,即单调递减区间;(Ⅱ)函数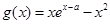 ,令
,令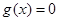 ,得
,得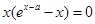 ,显然
,显然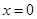 是一个零点,记
是一个零点,记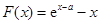 ,求导得
,求导得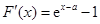 ,易知
,易知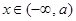 时
时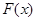 递减;
递减;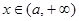 时
时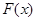 递增,故
递增,故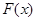 的最小值
的最小值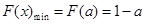 ,又
,又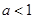 ,故
,故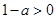 ,即
,即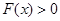 ,所以函数
,所以函数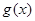 的零点个数1个.
的零点个数1个.
试题解析:(Ⅰ)解:因为 ,
,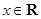 ,所以
,所以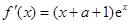 .
.
令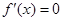 ,得
,得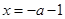 .当
.当 变化时,
变化时, 和
和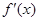 的变化情况如下:
的变化情况如下:
故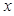
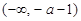
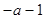
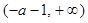
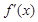

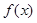
↘ ↗  的单调减区间为
的单调减区间为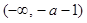 ;单调增区间为
;单调增区间为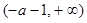 .
.
(Ⅱ)解:结论:函数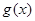 有且仅有一个零点. 理由如下:
有且仅有一个零点. 理由如下:
由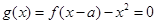 ,得方程
,得方程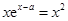 , 显然
, 显然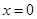 为此方程的一个实数解.
为此方程的一个实数解.
所以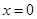 是函数
是函数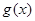 的一个零点. 当
的一个零点. 当
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
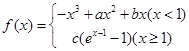 在
在 处存在极值.
处存在极值. 的值;
的值; 的图像上存在两点A,B使得
的图像上存在两点A,B使得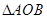 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在 轴上,求实数
轴上,求实数 的取值范围;
的取值范围; 时,讨论关于
时,讨论关于 的方程
的方程 的实根个数.
的实根个数.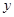 (升)关于行驶速度
(升)关于行驶速度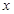 (千米/时)的函数可表示为
(千米/时)的函数可表示为 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 (升).
(升).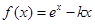 .
. ,且对于任意
,且对于任意 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围; ,
,
 ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的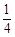 倍,固定成本为a元.
倍,固定成本为a元. .
. ,且对于任意
,且对于任意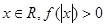 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围; ,求证:
,求证:
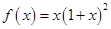 ,
,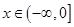 .
. 的极值点;
的极值点;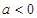 ,记
,记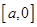 上的最小值为
上的最小值为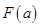 ,求
,求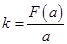 的最小值.
的最小值.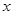 的函数
的函数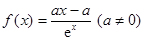
 时,求函数
时,求函数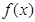 的极值;
的极值;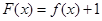 没有零点,求实数
没有零点,求实数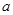 取值范围.
取值范围. ,
, .若函数
.若函数 依次在
依次在 处取到极值.
处取到极值. 的取值范围;
的取值范围; ,求
,求