题目内容
已知函数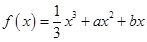
 .
.
(1)若曲线 经过点
经过点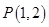 ,曲线
,曲线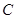 在点
在点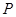 处的切线与直线
处的切线与直线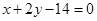 垂直,求
垂直,求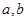 的值;
的值;
(2)在(1)的条件下,试求函数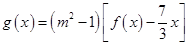 (
(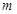 为实常数,
为实常数, )的极大值与极小值之差;
)的极大值与极小值之差;
(3)若 在区间
在区间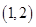 内存在两个不同的极值点,求证:
内存在两个不同的极值点,求证: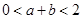 .
.
(1)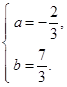
(2)当 或
或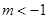 时,
时,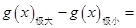
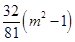 ;
;
当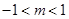 时,
时,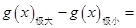
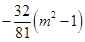 ;
;
(3)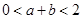 .
.
解析试题分析:(1)利用导数的几何意义,明确曲线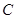 在点
在点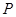 处的切线的斜率为
处的切线的斜率为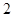 ,建立方程
,建立方程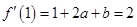 ,再根据曲线
,再根据曲线 经过点
经过点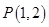 ,得到方程
,得到方程 ,解方程组即得所求.
,解方程组即得所求.
(2)利用“表解法”,确定函数的极值,注意讨论 或
或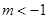 及
及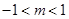 ,的不同情况;
,的不同情况;
(3)根据 在区间
在区间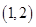 内存在两个极值点,得到
内存在两个极值点,得到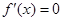 ,
,
即 在
在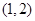 内有两个不等的实根.
内有两个不等的实根.
利用二次函数的图象和性质建立不等式组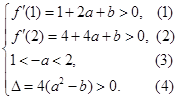 求
求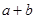 的范围.
的范围.
试题解析:(1)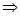
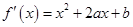 ,
, 直线
直线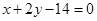 的斜率为
的斜率为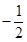 ,
, 曲线
曲线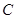 在点
在点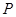 处的切线的斜率为
处的切线的斜率为 ,
, ①
①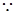 曲线
曲线 经过点
经过点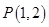 ,
,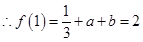 ②
②
由①②得: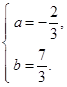 3分
3分
(2)由(1)知: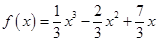 ,
,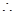
 ,
,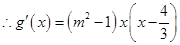 , 由
, 由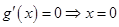 ,或
,或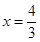 .
.
当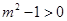 ,即
,即 或
或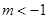 时,
时,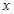 ,
,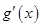 ,
,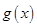 变化如下表
变化如下表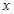
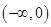

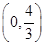
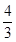
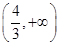
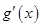
+ 0  练习册系列答案
练习册系列答案
西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
萌齐小升初强化模拟训练系列答案
相关题目
 ,其中a为正实数.
,其中a为正实数. 时,求f(x)的极值点.
时,求f(x)的极值点. ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围. .
. 存在单调递减区间,求实数
存在单调递减区间,求实数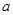 的取值范围;
的取值范围; ,求证:当
,求证:当 时,
时, 恒成立;
恒成立;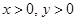 ,证明:
,证明: .
.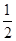 ax2-(2a+1)x+2ln x,a∈R.
ax2-(2a+1)x+2ln x,a∈R. .
. ,求函数
,求函数 的单调区间;
的单调区间; 图像上任意一点
图像上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. ax3-
ax3-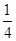 x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.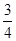 x2-bx+
x2-bx+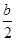 -
- -1.
-1.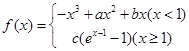 在
在 处存在极值.
处存在极值. 的值;
的值; 的图像上存在两点A,B使得
的图像上存在两点A,B使得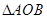 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在 轴上,求实数
轴上,求实数 的取值范围;
的取值范围; 时,讨论关于
时,讨论关于 的方程
的方程 的实根个数.
的实根个数.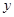 (升)关于行驶速度
(升)关于行驶速度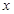 (千米/时)的函数可表示为
(千米/时)的函数可表示为 .已知甲、乙两地相距
.已知甲、乙两地相距 千米,在匀速行驶速度不超过
千米,在匀速行驶速度不超过 (升).
(升).