题目内容
sin2(π-α)+cos(-α)•sin(
-α)的值为( )
| π |
| 2 |
| A、cos2α |
| B、2sin2α |
| C、1 |
| D、0 |
考点:三角函数的化简求值,运用诱导公式化简求值
专题:三角函数的求值
分析:根据诱导公式和平方关系化简原式即可.
解答:
解:sin2(π-α)+cos(-α)•sin(
-α)
=sin2α+cosα•cosα=1,
故选:C.
| π |
| 2 |
=sin2α+cosα•cosα=1,
故选:C.
点评:本题考查利用诱导公式和平方关系对三角函数化简求值,属于基础题.

练习册系列答案
相关题目
若y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的最小值巍峨-2,其图象相邻最高点与最低点横坐标之差为2π,且图象过点(0,1),则其解析式是( )
| π |
| 2 |
A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(x+
| ||||
D、y=2sin(x+
|
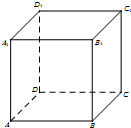 已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题:
已知正方体ABCD-A1B1C1D1的棱长为1.给出下列五个命题: