题目内容
8.记等差数列{an}的前n项和为Sn,若${a_1}=\frac{1}{2},{S_4}=20$,则d=3,S6=48.分析 利用等差数列的通项公式与求和公式即可得出.
解答 解:设等差数列{an}的公差为d,∵${a_1}=\frac{1}{2},{S_4}=20$,∴$4×\frac{1}{2}$+$\frac{4×3}{2}$d=20,解得d=3.
∴S6=$6×\frac{1}{2}+\frac{6×5}{2}×3$=48.
故答案为:3,48.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知${(1+x)^{10}}={a_0}+{a_1}(1-x)+{a_2}{(1-x)^2}+…+{a_{10}}{(1-x)^{10}}$,则a9等于( )
| A. | -10 | B. | 10 | C. | -20 | D. | 20 |
17.设集合A={1,2,3},B={y|y=x-1,x∈A},则A∪B等于( )
| A. | {1,2} | B. | {2,3} | C. | {0,1,2,3} | D. | {1,2,3,4} |
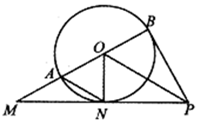 如图所示,已知AB为⊙O的直径,PB、PN都是⊙O的切线,切点分别为B、N,PN交BA的延长线于点M.
如图所示,已知AB为⊙O的直径,PB、PN都是⊙O的切线,切点分别为B、N,PN交BA的延长线于点M.