题目内容
(本小题满分12分)
已知矩形 与正三角形
与正三角形 所在的平面互相垂直,
所在的平面互相垂直,  、
、 分别为棱
分别为棱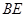 、
、 的中点,
的中点, ,
, ,
,
(1)证明:直线 平面
平面 ;
;
(2)求二面角 的大小.
的大小.
已知矩形
 与正三角形
与正三角形 所在的平面互相垂直,
所在的平面互相垂直,  、
、 分别为棱
分别为棱 、
、 的中点,
的中点, ,
, ,
,(1)证明:直线
 平面
平面 ;
;(2)求二面角
 的大小.
的大小.
(1)见解析;(2) .
.
 .
.(1)取EC的中点F,连接FM,FN,则可以证明四边形AMFN为平行四边形,从而证明AM//NF,问题得证.
(2)可以采用传统方法找(或作)出二面角的平面角,也可以考虑用空间向量法求二面角.
方法一:(1)证明:取EC的中点F,连接FM,FN,
则 ,
, ,
, ,
, ………………………2分
………………………2分
所以 且
且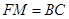 ,所以四边形
,所以四边形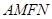 为平行四边形,
为平行四边形,
所以 , …………………………………4分
, …………………………………4分
因为 平面
平面 ,
,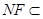 平面
平面 ,
,
所以直线 平面
平面 ; …………………………………6分
; …………………………………6分
 (2)解:由题设知面
(2)解:由题设知面 面
面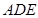 ,
, ,
,
又 ,∴面
,∴面 ,作
,作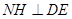 于
于 ,则
,则 ,作
,作 ,连接
,连接 ,由三垂线定理可知
,由三垂线定理可知 ,
,
∴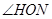 就是二面角
就是二面角 的平面角, …………………………………9分
的平面角, …………………………………9分
在正 中,可得
中,可得 ,在
,在 中,可得
中,可得 ,故在
,故在 中,
中, , ………………………………11分
, ………………………………11分
所以二面角 的大小为
的大小为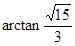 …………………………12分
…………………………12分

方法二:如图以N为坐标原点建立空间右手
直角坐标系,所以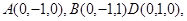
 …1分
…1分
(1)取EC的中点F,所以 ,
,
设平面 的一个法向量为
的一个法向量为 ,
,
因为 ,
,
所以 ,
,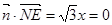 ;
; ,………3分
,………3分
因为 ,
, ,所以
,所以 ………………………5分
………………………5分
因为 平面
平面 ,所以直线
,所以直线 平面
平面 ………………………7分
………………………7分
(2)设平面 的一个法向量为
的一个法向量为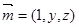 ,因为
,因为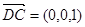 ,
,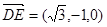
所以 ,
, ;所以
;所以 ……………9分
……………9分
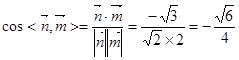 ………………………………11分
………………………………11分
因为二面角 的大小为锐角,
的大小为锐角,
所以二面角 的大小为
的大小为  ………………………………12分
………………………………12分
(2)可以采用传统方法找(或作)出二面角的平面角,也可以考虑用空间向量法求二面角.
方法一:(1)证明:取EC的中点F,连接FM,FN,
则
 ,
, ,
,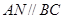 ,
, ………………………2分
………………………2分所以
 且
且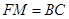 ,所以四边形
,所以四边形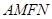 为平行四边形,
为平行四边形,所以
 , …………………………………4分
, …………………………………4分因为
 平面
平面 ,
,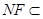 平面
平面 ,
,所以直线
 平面
平面 ; …………………………………6分
; …………………………………6分 (2)解:由题设知面
(2)解:由题设知面 面
面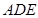 ,
, ,
,
又
 ,∴面
,∴面 ,作
,作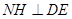 于
于 ,则
,则 ,作
,作 ,连接
,连接 ,由三垂线定理可知
,由三垂线定理可知 ,
,∴
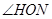 就是二面角
就是二面角 的平面角, …………………………………9分
的平面角, …………………………………9分在正
 中,可得
中,可得 ,在
,在 中,可得
中,可得 ,故在
,故在 中,
中, , ………………………………11分
, ………………………………11分所以二面角
 的大小为
的大小为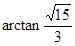 …………………………12分
…………………………12分
方法二:如图以N为坐标原点建立空间右手
直角坐标系,所以
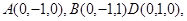
 …1分
…1分(1)取EC的中点F,所以
 ,
, 设平面
 的一个法向量为
的一个法向量为 ,
,因为
 ,
,
所以
 ,
,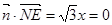 ;
; ,………3分
,………3分因为
 ,
, ,所以
,所以 ………………………5分
………………………5分因为
 平面
平面 ,所以直线
,所以直线 平面
平面 ………………………7分
………………………7分(2)设平面
 的一个法向量为
的一个法向量为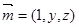 ,因为
,因为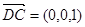 ,
,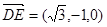
所以
 ,
, ;所以
;所以 ……………9分
……………9分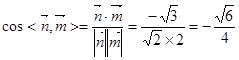 ………………………………11分
………………………………11分因为二面角
 的大小为锐角,
的大小为锐角,所以二面角
 的大小为
的大小为  ………………………………12分
………………………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的底面边长为
的底面边长为 ,
, 为
为 中点.
中点.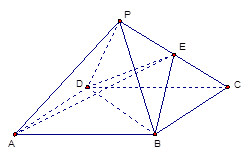
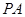 //平面
//平面 ;
; 是二面角
是二面角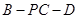 的平面角,求直线
的平面角,求直线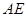 与平面
与平面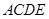 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
. 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;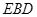 与平面
与平面 的余弦值。
的余弦值。
 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。 平面
平面 ;
; 的正切值的大小。(12分)
的正切值的大小。(12分)
 、
、 、
、 和直线
和直线 、
、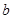 、m、n,下列命题中真命题是
、m、n,下列命题中真命题是 ,则
,则
 ,则
,则
 ,则
,则
 则
则
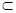 平面α,直线c
平面α,直线c 为两条不同的直线,
为两条不同的直线,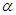 、
、 为两个不同的平面,则下列命题正确的是
为两个不同的平面,则下列命题正确的是 ;
;


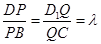 .
. 的值.
的值.
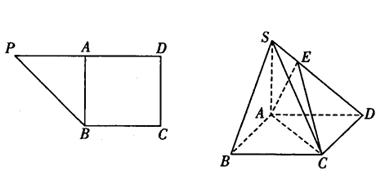
 ,将
,将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下右图。
,如下右图。 平面ABCD;(2)求二面角E—AC—D的正切值.
平面ABCD;(2)求二面角E—AC—D的正切值.