题目内容
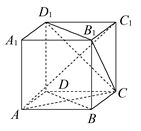
(12分)如图已知直角梯形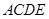 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
.
(I)在直线 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;
(II)求平面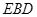 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值。
的余弦值。

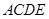 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
, .
.(I)在直线
 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;(II)求平面
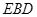 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值。
的余弦值。
(I)见解析;(2)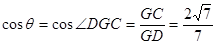 .
.
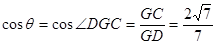 .
. (1)先确定线段 的中点就是满足条件的点
的中点就是满足条件的点 .再取
.再取 的中点
的中点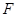 ,证明四边形
,证明四边形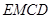 为矩形,四边形
为矩形,四边形 是平行四边形.由线面平行的判定定理证出结论;
是平行四边形.由线面平行的判定定理证出结论;
(2)可以根据二面角的定义找出二面角的平面角求解,关键是找到二面角的棱,由平面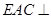 平面
平面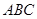 ,
,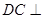 平面
平面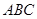 ,
, 。∴
。∴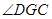 是所求二面角的平面角.在三角形中求解;也可以建立坐标系利用法向量求解。
是所求二面角的平面角.在三角形中求解;也可以建立坐标系利用法向量求解。
(I)线段 的中点就是满足条件的点
的中点就是满足条件的点 .
.

证明如下:
取 的中点
的中点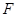 连结
连结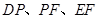 ,则
,则
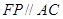 ,
,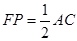 , …………………2分
, …………………2分
取 的中点
的中点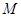 ,连结
,连结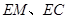 ,
,
∵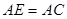 且
且 ,
,
∴△ 是正三角形,∴
是正三角形,∴ .
.
∴四边形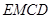 为矩形,∴
为矩形,∴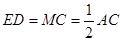 .又∵
.又∵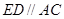 ,………3分
,………3分
∴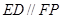 且
且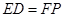 ,四边形
,四边形 是平行四边形.…………4分
是平行四边形.…………4分
∴ ,而
,而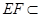 平面
平面 ,
,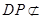 平面
平面 ,∴
,∴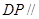 平面
平面 .……6分
.……6分
(2)(法1)过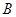 作
作 的平行线
的平行线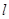 ,过
,过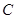 作
作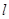 的垂线交
的垂线交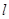 于
于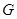 ,连结
,连结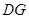 ,∵
,∵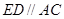 ,∴
,∴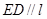 ,
, 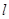 是平面
是平面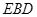 与平面
与平面 所成二面角的棱.……8分
所成二面角的棱.……8分
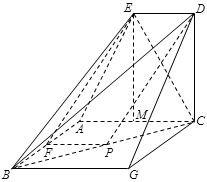
∵平面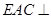 平面
平面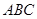 ,
, ,∴
,∴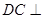 平面
平面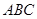 ,
,
又∵ 平面
平面 ,
,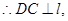 ∴
∴ 平面
平面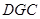 ,∴
,∴ ,
,
∴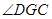 是所求二面角的平面角.………………10分
是所求二面角的平面角.………………10分
设 ,则
,则 ,
,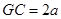 ,
,
∴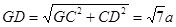 ,
,
∴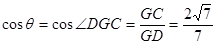 . ………12分
. ………12分
(法2)∵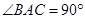 ,平面
,平面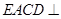 平面
平面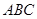 ,
,
∴以点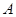 为原点,直线
为原点,直线 为
为 轴,直线
轴,直线 为
为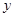 轴,建立空间直角坐标系
轴,建立空间直角坐标系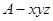 ,则
,则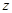 轴在平面
轴在平面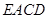 内(如图).设
内(如图).设 ,由已知,得
,由已知,得 ,
,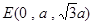 ,
, .
.

∴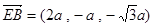 ,
,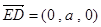 ,…………………8分
,…………………8分
设平面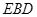 的法向量为
的法向量为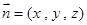 ,
,
则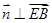 且
且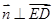 ,
,
∴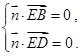 ∴
∴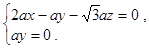 解之得
解之得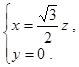
取 ,得平面
,得平面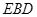 的一个法向量为
的一个法向量为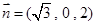 . ………10分
. ………10分
又∵平面 的一个法向量为
的一个法向量为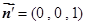 . ……11分
. ……11分
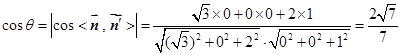 .………12分
.………12分
 的中点就是满足条件的点
的中点就是满足条件的点 .再取
.再取 的中点
的中点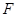 ,证明四边形
,证明四边形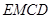 为矩形,四边形
为矩形,四边形 是平行四边形.由线面平行的判定定理证出结论;
是平行四边形.由线面平行的判定定理证出结论;(2)可以根据二面角的定义找出二面角的平面角求解,关键是找到二面角的棱,由平面
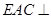 平面
平面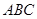 ,
,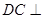 平面
平面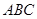 ,
, 。∴
。∴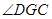 是所求二面角的平面角.在三角形中求解;也可以建立坐标系利用法向量求解。
是所求二面角的平面角.在三角形中求解;也可以建立坐标系利用法向量求解。(I)线段
 的中点就是满足条件的点
的中点就是满足条件的点 .
.
证明如下:
取
 的中点
的中点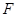 连结
连结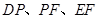 ,则
,则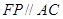 ,
,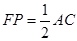 , …………………2分
, …………………2分取
 的中点
的中点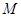 ,连结
,连结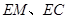 ,
,∵
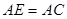 且
且 ,
,∴△
 是正三角形,∴
是正三角形,∴ .
.∴四边形
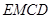 为矩形,∴
为矩形,∴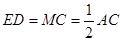 .又∵
.又∵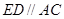 ,………3分
,………3分∴
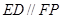 且
且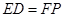 ,四边形
,四边形 是平行四边形.…………4分
是平行四边形.…………4分∴
 ,而
,而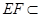 平面
平面 ,
,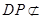 平面
平面 ,∴
,∴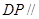 平面
平面 .……6分
.……6分(2)(法1)过
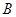 作
作 的平行线
的平行线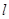 ,过
,过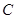 作
作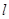 的垂线交
的垂线交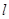 于
于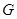 ,连结
,连结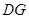 ,∵
,∵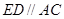 ,∴
,∴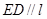 ,
, 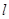 是平面
是平面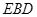 与平面
与平面 所成二面角的棱.……8分
所成二面角的棱.……8分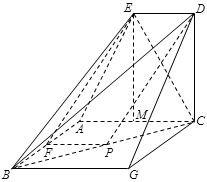
∵平面
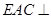 平面
平面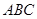 ,
, ,∴
,∴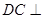 平面
平面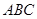 ,
,又∵
 平面
平面 ,
,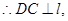 ∴
∴ 平面
平面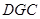 ,∴
,∴ ,
,∴
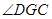 是所求二面角的平面角.………………10分
是所求二面角的平面角.………………10分设
 ,则
,则 ,
,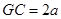 ,
,∴
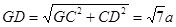 ,
,∴
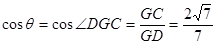 . ………12分
. ………12分(法2)∵
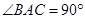 ,平面
,平面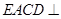 平面
平面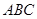 ,
,∴以点
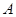 为原点,直线
为原点,直线 为
为 轴,直线
轴,直线 为
为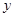 轴,建立空间直角坐标系
轴,建立空间直角坐标系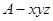 ,则
,则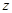 轴在平面
轴在平面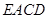 内(如图).设
内(如图).设 ,由已知,得
,由已知,得 ,
,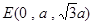 ,
, .
.
∴
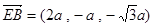 ,
,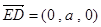 ,…………………8分
,…………………8分设平面
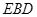 的法向量为
的法向量为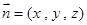 ,
,则
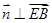 且
且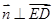 ,
,∴
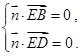 ∴
∴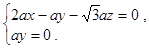 解之得
解之得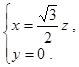
取
 ,得平面
,得平面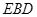 的一个法向量为
的一个法向量为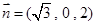 . ………10分
. ………10分又∵平面
 的一个法向量为
的一个法向量为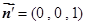 . ……11分
. ……11分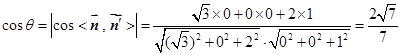 .………12分
.………12分 
练习册系列答案
相关题目
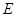 ,
,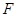 分别是正方形
分别是正方形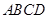 边
边 、
、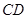 的中点,
的中点, 与
与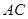 交于点
交于点 ,
,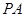 、
、 都垂直于平面
都垂直于平面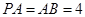 ,
,  ,
,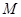 是线段
是线段
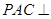 平面
平面 ;
; 平面
平面 ;
;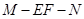 的余弦值.
的余弦值.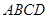 和正
和正
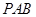 所在平面互相垂直,其中
所在平面互相垂直,其中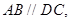
 ,且
,且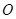 为
为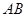 中点.
中点. 
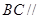 平面
平面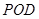 ;
;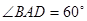 ,求二面角
,求二面角 的余弦值;
的余弦值;
 与正三角形
与正三角形 所在的平面互相垂直,
所在的平面互相垂直,  、
、 分别为棱
分别为棱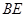 、
、 的中点,
的中点, ,
, ,
, 平面
平面 ;
; 的大小.
的大小.
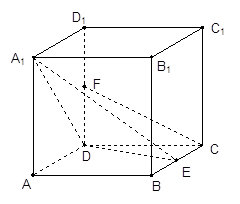
 ,则
,则


 ,
,

 ,
, ,则
,则