题目内容
已知 为两条不同的直线,
为两条不同的直线,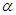 、
、 为两个不同的平面,则下列命题正确的是
为两个不同的平面,则下列命题正确的是
 为两条不同的直线,
为两条不同的直线,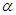 、
、 为两个不同的平面,则下列命题正确的是
为两个不同的平面,则下列命题正确的是A. ; ; | B. |
C. | D. |
D
解:
A. ;只哟当两直线相交时成立
;只哟当两直线相交时成立
B. ,两个平面平行,并不是说两平面内任何一条直线都平行,可能异面。错误
,两个平面平行,并不是说两平面内任何一条直线都平行,可能异面。错误
C. 可能n在平面内,错误
可能n在平面内,错误
D. ,两条平行线中的一条垂直于该平面,则另一条也垂直于该平面。
,两条平行线中的一条垂直于该平面,则另一条也垂直于该平面。
A.
 ;只哟当两直线相交时成立
;只哟当两直线相交时成立B.
 ,两个平面平行,并不是说两平面内任何一条直线都平行,可能异面。错误
,两个平面平行,并不是说两平面内任何一条直线都平行,可能异面。错误C.
 可能n在平面内,错误
可能n在平面内,错误D.
 ,两条平行线中的一条垂直于该平面,则另一条也垂直于该平面。
,两条平行线中的一条垂直于该平面,则另一条也垂直于该平面。
练习册系列答案
相关题目
 的底面为菱形,且
的底面为菱形,且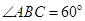 ,
,
 .
.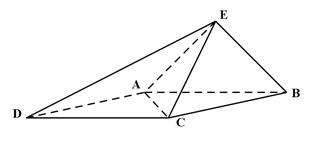
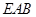
 平面
平面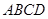 ;
; 的余弦值.
的余弦值.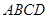 和正
和正
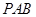 所在平面互相垂直,其中
所在平面互相垂直,其中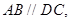
 ,且
,且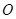 为
为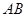 中点.
中点. 
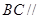 平面
平面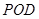 ;
;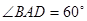 ,求二面角
,求二面角 的余弦值;
的余弦值; 与正三角形
与正三角形 所在的平面互相垂直,
所在的平面互相垂直,  、
、 分别为棱
分别为棱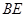 、
、 的中点,
的中点, ,
, ,
, 平面
平面 ;
; 的大小.
的大小.
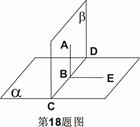
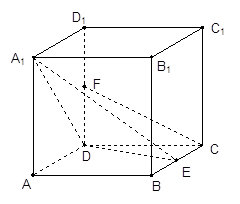

 中,已知
中,已知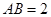 ,
,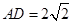 ,
, 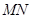 分别为
分别为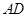 和
和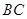 的中点,对角线
的中点,对角线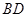 与
与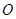 点,沿
点,沿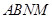 折起,使平面
折起,使平面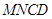 所成角为
所成角为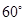 ,如图5(2).
,如图5(2).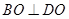 ;
;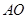 与平面
与平面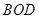 所成角的正弦值.
所成角的正弦值.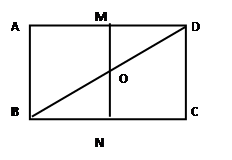

 表示平面,m,n表示直线,则m//
表示平面,m,n表示直线,则m// 的一个充分条件是( )
的一个充分条件是( ) 


