题目内容
 一个三棱锥的三视图如图所示,其正视图、侧视图、俯视图面积分别是3、4、6,由这个几何体外接球表面积为
一个三棱锥的三视图如图所示,其正视图、侧视图、俯视图面积分别是3、4、6,由这个几何体外接球表面积为分析:几何体是一个三棱锥,一条侧棱与底面垂直,底面是一个直角三角形,根据正视图、侧视图、俯视图面积分别是3、4、6.求出三条边的长度,这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,做出长方体的直径,求出球的表面积.
解答:解:由题意知几何体是一个三棱锥,一条侧棱与底面垂直,
底面是一个直角三角形,
∵正视图、侧视图、俯视图面积分别是3、4、6
设出三条互相垂直的棱长是x,y,z,
有xz=6,yz=8,xy=12,
∴x=3,y=4,z=2
这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,
长方体的直径是
=
,
∴几何体的外接球的表面积是29π,
故答案为:29π
底面是一个直角三角形,
∵正视图、侧视图、俯视图面积分别是3、4、6
设出三条互相垂直的棱长是x,y,z,
有xz=6,yz=8,xy=12,
∴x=3,y=4,z=2
这个三棱锥的外接球也是以这个三棱锥三条侧棱为棱的长方体的外接球,
长方体的直径是
| 4+9+16 |
| 29 |
∴几何体的外接球的表面积是29π,
故答案为:29π
点评:本题考查球和几何体之间的关系,本题解题的关键是根据三条侧棱两两垂直的关系得到由这三条侧棱构成的长方体,从而得到外接球的表面积.

练习册系列答案
相关题目
 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为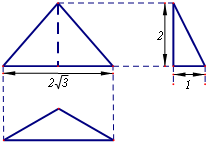 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为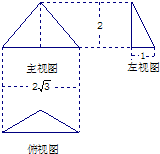 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为 (2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )
(2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )