Question

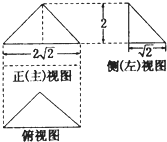
已知一个三棱锥的三视图如图所示，其中俯视图是顶角为120°的等腰三角形，则该三棱锥的体积为

2 3

3

．

Answer 1

分析：根据已知中的三视图，可得该几何体是一个三棱锥，求出棱锥的底面面积及棱锥的高，代入棱锥体积公式，可得答案．

解答：解：由已知中的三视图可得，该几何体是一个三棱锥
由一视图和俯视图可得底面底边长为2

3

，
由左视图可得底面底边上的高为1，
故底面积S=

1

2

×2

3

×1=

3

由主视图和左视图可得棱锥的高h=2
故棱锥的体积V=

1

3

Sh=

1

3

×

3

×2=

2 3

3

故答案为：

2 3

3

点评：本题考查的知识点是由三视图求体积，其中根据已知中的三视图判断出几何体的形状是解答的关键．