题目内容
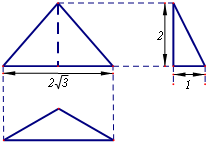 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的外接球体积为分析:几何体是一个底面是顶角为120°且底边长是2
,在等腰三角形的顶点处有一条垂直于底面的侧棱,侧棱长是2,建立适当的坐标系,写出各个点的坐标和设出球心的坐标,根据各个点到球心的距离相等,点的球心的坐标,点的半径,做出体积.
| 3 |
解答: 解:由三视图知,几何体是一个底面是顶角为120°且底边长是2
解:由三视图知,几何体是一个底面是顶角为120°且底边长是2
,底边上的高是1,
在等腰三角形的顶点处有一条垂直于底面的侧棱,侧棱长是2,
以D为原点,DB为x轴,DA为y轴,建立空间直角坐标系,
则D(0,0,0),A(0,0,2),B(2,0,0),C(-1,
,0)
∵(x-2)2+y2+z2=x2+y2+z2,①
x2+y2+(z-2)2=x2+y2+z2,②
(x+1)2+(y-
)2+z2=x2+y2+z2,③
∴x=1,y=
,z=1,
∴球心的坐标是(1,
,1),
∴球的半径是
=
∴球的体积是
π×(
)3=
,
故答案为:
 解:由三视图知,几何体是一个底面是顶角为120°且底边长是2
解:由三视图知,几何体是一个底面是顶角为120°且底边长是2| 3 |
在等腰三角形的顶点处有一条垂直于底面的侧棱,侧棱长是2,
以D为原点,DB为x轴,DA为y轴,建立空间直角坐标系,
则D(0,0,0),A(0,0,2),B(2,0,0),C(-1,
| 3 |
∵(x-2)2+y2+z2=x2+y2+z2,①
x2+y2+(z-2)2=x2+y2+z2,②
(x+1)2+(y-
| 3 |
∴x=1,y=
| 3 |
∴球心的坐标是(1,
| 3 |
∴球的半径是
12+(
|
| 5 |
∴球的体积是
| 4 |
| 3 |
| 5 |
20
| ||
| 3 |
故答案为:
20
| ||
| 3 |
点评:本题考查由三视图求几何体的体积,考查由三视图还原几何体,考查三棱锥与外接球之间的关系,考查利用空间向量解决立体几何问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
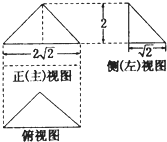 已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为( )
已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为( )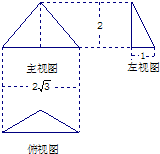 已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为
已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,则该三棱锥的体积为 已知一个三棱锥的三视图如图所示,其中主视图、俯视图是全等的等腰直角三角形,则该三棱锥的外接球体积为
已知一个三棱锥的三视图如图所示,其中主视图、俯视图是全等的等腰直角三角形,则该三棱锥的外接球体积为 (2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )
(2013•东城区二模)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( )