题目内容
17．已知全集U=R，集合$A=\left\{{x\left|{\frac{x+2}{x}＜0}\right.}\right\}$，则集合∁UA={x|x≥0或x≤-2}．分析 求出集合的等价条件，结合补集的定义进行求解即可．
解答 解：$A=\left\{{x\left|{\frac{x+2}{x}＜0}\right.}\right\}$={x|-2＜x＜0}，
则∁UA={x|x≥0或x≤-2}，
故答案为：{x|x≥0或x≤-2}
点评 本题主要考查集合的基本运算，先求出集合A，根据补集定义进行求解是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
8．设命题p：?x∈R，x2＜2015，则￢p为（ ）
| A． | ?x∈R，x2≥2015 | B． | ?x∈R，x2＜2015 | C． | ?x∈R，x2≥2015 | D． | ?x∈R，x2＞2015 |
5．
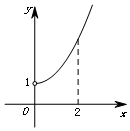已知函数y=f（x）（x∈R）是奇函数，其部分图象如图所示，则在（-2，0）上与函数f（x）的单调性相同的是（ ）
已知函数y=f（x）（x∈R）是奇函数，其部分图象如图所示，则在（-2，0）上与函数f（x）的单调性相同的是（ ）| A． | y=x2+1 | B． | y=log2|x| | ||
| C． | y=$\left\{\begin{array}{l}{{e}^{x}（x≥0）}\\{{e}^{-x}（x＜0）}\end{array}\right.$ | D． | y=|x+2| |
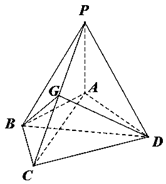如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=BC=2，$AD=CD=\sqrt{7}$，$PA=\sqrt{3}$，∠ABC=120°，G为线段PC上的点．