Question

【题目】已知二次函数(其中)满足下列三个条件:①图象过坐标原点;②对于任意都成立;③方程有两个相等的实数根.

(1)求函数的解析式;

(2)令(其中)，求函数的单调区间(直接写出结果即可);

(3)研究方程在区间内的解的个数.

Answer 1

【答案】（1）；（2）见解析；（3）见解析

【解析】

（1）由图象过原点得，由得对称轴，方程有两个相等实根，对应的，三个条件可得三个等式，从而求得得解析式；

（2）化简函数为分段函数，当时，结合函数的对称轴求出单调区间，时类似求出单调区间．

（3）结合（2）中函数的单调性可研究在上的零点个数．注意零点存在定理的应用．

（1）因为图象过坐标原点，所以，即，

又，所以其对称轴是，即，，

又方程为，即有两个相等实根，所以，，

所以．

（2），

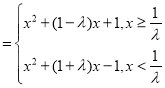①当时，的对称轴是，

若，即时，在上单调递增，

若，即时，在上单调递增，在上递减，

②当时，的对称轴是，

则函数在上递减，在上递增，

综上所述，当时，的减区间为，增区间为；时，减区间为，，增区间为，．

（3）①当时，由（2）知在上单调递增，

又，，故函数在上只有一个零点；

②时，则，，，，

（i）当时，，

且，此时在上只有一个零点，

（ii）当时，且，此时在上有两个不同零点．

综上所述，当时，在上只有一个零点，时，在上有两个不同零点．