题目内容
【题目】已知向量![]() ,
,![]() 函数
函数![]() .
.
(1)将函数![]() 的图像向右平移m(
的图像向右平移m(![]() )个单位长度,所得图像对应的函数为奇函数,写出m的最小值(不要求写过程);
)个单位长度,所得图像对应的函数为奇函数,写出m的最小值(不要求写过程);
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() (
(![]() )在区间
)在区间![]() 上是单调递增函数,求正数
上是单调递增函数,求正数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)对![]() 进行化简,再得到平移后的函数,根据奇函数表示出其对称中心,得到
进行化简,再得到平移后的函数,根据奇函数表示出其对称中心,得到![]() 的表达式,从而得到
的表达式,从而得到![]() 的值;(2)根据题意得到
的值;(2)根据题意得到![]() 的值,再根据
的值,再根据![]() 的范围,得到
的范围,得到![]() 的值,然后将所求的
的值,然后将所求的![]() 转化为
转化为![]() ,根据两角差的余弦公式,得到答案;(3)根据
,根据两角差的余弦公式,得到答案;(3)根据![]() 的范围,得到
的范围,得到![]() 的范围,根据在
的范围,根据在![]() 上单调递增,得到
上单调递增,得到![]() 的范围,结合
的范围,结合![]() 的取值,得到答案.
的取值,得到答案.
(1)![]()
![]()
向右平移m(![]() )个单位长度,
)个单位长度,
得![]() ,
,
因为是奇函数,所以其对称中心为![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() .
.
得到![]() ,
,![]() ,
,
所以![]() 的最小值是
的最小值是![]() .
.
(2)![]() ,
,
即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以 ,
,
![]()
![]() .
.
(3)![]() ,
,
当![]() 时,
时,![]() ,
,
于是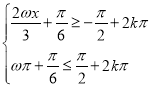 ,
,![]() ,
,
解得 ,
,![]() ,
,
所以当![]() 时,
时, ,当
,当![]() 时,
时,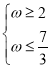
当![]() 时,无解集,
时,无解集,
而![]() ,
,
所以得![]() 或
或![]() .
.
所以![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目