题目内容
【题目】已知二次函数
满足条件
是偶函数， 
，且
的图象与直线
恰有一个公共点.
（1）求的解析式；
（2）设
，是否存在实数
，使得函数
在区间
上的最大值为2？如果存在，求出的值；如果不存在，请说明理由.
【答案】（1）
；（2）
或
.
【解析】
（1）根据
是偶函数、
、
与
仅有一交点，得到对应的方程组，求解出
的值即可求解出的解析式；
（2）根据
的对称轴，利用轴定区间动进行分类讨论，由此确定出符合条件的
的取值.
（1）因为是偶函数，所以的对称轴为
，所以
，
又因为，所以
，
又因为与仅有一交点，所以
仅有一根，所以
，
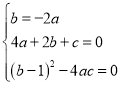所以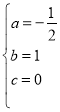
，所以
，所以；
（2）因为
，所以的对称轴
，
当
时即
，在
上单调递减，
所以
，解得：或
（舍）；
当
时，在上单调递增，
所以
，解得：或
（舍）；
当
时，在
上递增，在
上递减，
所以
，此时不满足.
综上可知：或.
练习册系列答案
计算高手系列答案
相关题目
