题目内容
在平面直角坐标系中,曲线C1的参数方程为:
(φ为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ=2cosθ
(1)去曲线C1的直角坐标方程;
(2)已知点M是曲线C1上任意一点,点N是曲线C2上任意一点,求|MN|的取值范围.
|
(1)去曲线C1的直角坐标方程;
(2)已知点M是曲线C1上任意一点,点N是曲线C2上任意一点,求|MN|的取值范围.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)直接根据极坐标和直角坐标互化公式求解即可;
(2)利用已知,得到|MC2|-1≤|MN|≤|MC2|+1,然后,得到|MC2|2=(4cosφ-1)2+9sin2φ=7cos2φ-8cosφ+10,借助于三角函数的取值情况进行求解即可.
(2)利用已知,得到|MC2|-1≤|MN|≤|MC2|+1,然后,得到|MC2|2=(4cosφ-1)2+9sin2φ=7cos2φ-8cosφ+10,借助于三角函数的取值情况进行求解即可.
解答:
解:(1)由ρ=2cosθ,得
ρ2=2ρcosθ,
∴x2+y2=2x,
∴(x-1)2+y2=1,
(2)设点M(4cosφ,3sinφ),则
|MC2|-1≤|MN|≤|MC2|+1,
|MC2|2=(4cosφ-1)2+9sin2φ=7cos2φ-8cosφ+10,
当cosφ=-1时,得|MC2|2max=25,|MC2|max=5,
当cosφ=
时,得|MC2|2min=
,|MC2|min=
,
∴
-1≤|MC2|-1≤|MN|≤|MC2|+1≤5+1,
∴|MN|的取值范围[
-1,6].
ρ2=2ρcosθ,
∴x2+y2=2x,
∴(x-1)2+y2=1,
(2)设点M(4cosφ,3sinφ),则
|MC2|-1≤|MN|≤|MC2|+1,
|MC2|2=(4cosφ-1)2+9sin2φ=7cos2φ-8cosφ+10,
当cosφ=-1时,得|MC2|2max=25,|MC2|max=5,
当cosφ=
| 4 |
| 7 |
| 54 |
| 7 |
3
| ||
| 7 |
∴
3
| ||
| 7 |
∴|MN|的取值范围[
3
| ||
| 7 |
点评:本题重点考查极坐标和直角坐标的互化公式、距离问题处理思路和方法等知识,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
已知一组数1,1,2,3,5,8,x,21,34,55,按这组数规律,x应为( )
| A、11 | B、12 | C、13 | D、14 |
七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙,丙两位同学要站在一起,则不同的排法有( )
| A、240种 | B、192种 |
| C、120种 | D、96种 |
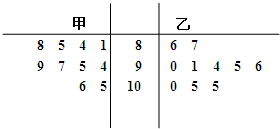 甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分
甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=kx-1,其中实数k随机选自区间[-2,2],?x∈[0,1],f(x)≤0的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=
不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
|
| A、(-2,0) |
| B、(-∞,0) |
| C、(0,2) |
| D、(-∞,-2) |
若函数f(x)=
sin(2x+θ)+cos(2x+θ)为奇函数,且在[-
,0]上为减函数,则θ的一个值为( )
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|