题目内容
2. 已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x,现已画出函数f(x)在y轴左侧的图象,如图所示.
已知函数f(x)是定义在R上的奇函数,且当x≤0时,f(x)=x2+2x,现已画出函数f(x)在y轴左侧的图象,如图所示.(1)补充完成f(x)的图象,并求函数f(x),x∈R的解析式;
(2)若函数g(x)=f(2x)+2,x∈[-1,1]的值域;
(3)求解关于x的不等式f(3x-3)>0.
分析 (1)根据奇函数图象的对称性作图,利用f(x)=-f(-x)得出f(x)在(0,+∞)上的解析式;
(2)求出2x的范围,根据函数图象得出f(2x)的范围,从而得出g(x)的值域;
(3)根据函数图象列不等式求出解集.
解答 解:(1)当x>0时,-x<0,
∴f(-x)=(-x)2-2x=x2-2x,
又f(x)是奇函数,
∴f(x)=-f(-x)=-x2+2x.
∴f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≤0}\\{-{x}^{2}+2x,x>0}\end{array}\right.$
作出函数的图象如图所示: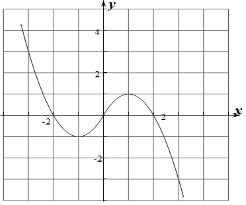
(2)∵x∈[-1,1],∴$\frac{1}{2}≤$2x≤2,
由图象可知f(x)在[$\frac{1}{2}$,1]上单调递增,在(1,2]上单调递减,
且f($\frac{1}{2}$)=$\frac{3}{4}$,f(1)=1,f(2)=0,
∴0≤f(2x)≤1,∴2≤f(2x)+2≤3.
即g(x)在[-1,1]上的值域为[2,3].
(3)由图象可知f(x)>0的解为x<-2或0<x<2,
∵f(3x-3)>0,
∴3x-3<-2或0<3x-3<2,
即3x<1或3<3x<5,
解得x<0或1<x<log35.
点评 本题考查了奇函数的性质,函数图象与不等式的解,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.若双曲线$\frac{{x}^{2}}{m-1}$-$\frac{{y}^{2}}{m}$=1(m>1)的虚轴长为6,则此双曲线的渐近线方程为( )
| A. | y=±$\frac{8}{9}$x | B. | y=±$\frac{2\sqrt{2}}{3}$x | C. | y=±$\frac{9}{8}$x | D. | y=±$\frac{3\sqrt{2}}{4}$x |
10.设函数f(x)是定义在(0,+∞)上的可导函数,其导函数为f′(x),且有2f(x)+xf′(x)>x2,则不等式(x-2014)2f(x-2014)-4f(2)>0的解集为( )
| A. | (2012,+∞) | B. | (0,2012) | C. | (0,2016) | D. | (2016,+∞) |
17.已知椭圆C1:$\frac{{x}^{2}}{5}$+y2=1与双曲线C2的公共焦点为F1,F2,A,B分别为C1,C2在第二、第四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
7.设非空集合A,B满足A⊆B,则以下表述正确的是( )
| A. | ?x0∈A,x0∈B | B. | ?x∈A,x∈B | C. | ?x0∈B,x0∉A | D. | ?x∈B,x∈A |
11.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≤x+1}\\{y≥2x-4}\\{x+2y≥2}\end{array}\right.$,则目标函数z=3x-2y的最大值为( )
| A. | 6 | B. | 3 | C. | 9 | D. | 2 |
12.设a>0,b>0,直线l1:ax+y=1,直线l2:x+by=1,若直线l1∥l2,则a+b的取值范围为( )
| A. | (0,2] | B. | (0,2) | C. | [2,+∞) | D. | (2,+∞) |