题目内容
11．设变量x，y满足约束条件$\left\{\begin{array}{l}{y≤x+1}\\{y≥2x-4}\\{x+2y≥2}\end{array}\right.$，则目标函数z=3x-2y的最大值为（ ）| A． | 6 | B． | 3 | C． | 9 | D． | 2 |
分析 作出约束条件$\left\{\begin{array}{l}{y≤x+1}\\{y≥2x-4}\\{x+2y≥2}\end{array}\right.$，对应的平面区域，利用z的几何意义，即可得到结论．
解答 解：作出约束条件$\left\{\begin{array}{l}{y≤x+1}\\{y≥2x-4}\\{x+2y≥2}\end{array}\right.$，对应的平面区域如图：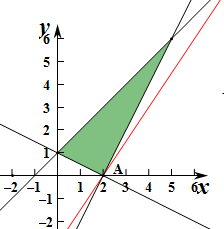
由z=3x-2y得y=$\frac{3}{2}$x-$\frac{z}{2}$，
平移直线y=$\frac{3}{2}$x-$\frac{z}{2}$当直线y=$\frac{3}{2}$x-$\frac{z}{2}$经过点A时，直线y=$\frac{3}{2}$x-$\frac{z}{2}$的截距最小，此时z最大．
由$\left\{\begin{array}{l}{y=2x-4}\\{x+2y=2}\end{array}\right.$，解得A（2，0），
此时zmax=3×2=6，
故选：A．
点评 本题主要考查线性规划的应用，利用z的几何意义，通过数形结合是解决本题的关键．
练习册系列答案
相关题目
1．为迎接“义务教育均衡检查”，某校在初中三个年级中开展“义务教育均衡”知晓情况调查，其中初中一年级共500人，初中二年级共650人，初中三年级共450人，现用分层抽样的方式在初中三个年级中共抽取32名同学进行调查，则初中一年级应抽取的人数为（ ）
| A． | 13 | B． | 9 | C． | 10 | D． | 12 |
已知函数f（x）是定义在R上的奇函数，且当x≤0时，f（x）=x2+2x，现已画出函数f（x）在y轴左侧的图象，如图所示．
19．已知正方体的8个顶点中，有4个为一侧面是等边三角形的正三棱锥的顶点，则这个正三棱锥与正方体的全面积之比可能为（ ）
| A． | $1：\sqrt{3}$ | B． | $1：\sqrt{2}$ | C． | $2：\sqrt{2}$ | D． | $3：\sqrt{6}$ |
6．已知α∩β=l，m是平面α内的任意直线，在平面β内总存在一条直线n，使下列命题一定正确的是（ ）
| A． | m与n相交 | B． | m与n平行 | C． | m与n垂直 | D． | l与m、n都异面 |
3．函数y=-2sin（2x+$\frac{π}{4}$）图象的一个对称中心是（ ）
| A． | （$\frac{π}{8}$，0） | B． | （-$\frac{π}{8}$，0） | C． | （$\frac{π}{4}$，0） | D． | （-$\frac{π}{4}$，0） |
1．海水受日月的引力，在一定的时候发生涨落的现象叫潮．一般地，早潮叫潮，晚潮叫汐．在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋．下面是某港口在某季节每天的时间与水深关系表：
（1）若用函数f（t）=Asin（ωt+φ）+h（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）来近似描述这个港口的水深和时间之间的对应关系，根据表中数据确定函数表达式；
（2）一条货船的吃水深度（船底与水面的距离）为4米，安全条例规定要有2.25米的安全间隙（船底与洋底的距离），该船何时能进入港口？
| 时刻（t） | 0：00 | 3：00 | 6：00 | 9：00 | 12：00 | 15：00 | 18：00 | 21：00 | 24：00 |
| 水深/米（y） | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 | 7.5 | 5.0 | 2.5 | 5.0 |
（2）一条货船的吃水深度（船底与水面的距离）为4米，安全条例规定要有2.25米的安全间隙（船底与洋底的距离），该船何时能进入港口？