题目内容
4.在锐角△ABC中,交A,B,C的对边分别是a,b,c,且A,B,C成等差数列(Ⅰ)若$\overrightarrow{BA}$$•\overrightarrow{BC}$=$\frac{3}{2}$,b=$\sqrt{3}$,求a+c的值;
(Ⅱ)求2sinA+sinC的取值范围.
分析 根据题意,求出B=60°,A+C=120°;
(Ⅰ)由数量积的定义得出c•a•cosB=$\frac{3}{2}$,求出ac的值,再利用余弦定理求出a2+c2的值,即可求出a+c;
(Ⅱ)利用三角恒等变换化简2sinA+sinC,根据C的范围求出2sinA+sinC的取值范围.
解答 解:锐角△ABC中,A、B、C成等差数列,
∴2B=A+C,
又A+B+C=180°,
∴B=60°,A+C=120°;
(Ⅰ)当$\overrightarrow{BA}$$•\overrightarrow{BC}$=$\frac{3}{2}$时,即c•a•cosB=$\frac{3}{2}$,
∴c•a•cos60°=$\frac{3}{2}$,
∴ac=3;
又b=$\sqrt{3}$,
∴b2=a2+c2-2accosB=a2+c2-2•$\frac{3}{2}$=3,
∴a2+c2=6;
∴(a+c)2=a2+c2+2ac=6+2×3=12,
∴a+c=2$\sqrt{3}$;
(Ⅱ)2sinA+sinC=2sin(120°-C)+sinC
=2sin120°cosC-2cos120°sinC+sinC
=$\sqrt{3}$cosC+2sinC
=$\sqrt{7}$sin(C+θ),且θ=arctan$\frac{\sqrt{3}}{2}$,30°<C<90°,
∴30°<θ<45°
∴60°<C+θ<135°,
∴$\frac{\sqrt{2}}{2}$<sin(C+θ)≤1,
∴$\frac{\sqrt{14}}{2}$<$\sqrt{7}$sin(C+θ)≤$\sqrt{7}$,
∴2sinA+sinC的取值范围是($\frac{\sqrt{14}}{2}$,$\sqrt{7}$].
点评 本题考查了平面向量以及三角恒等变换和余弦定理的应用问题,解题的关键是充分利用余弦定理的性质,是综合性题目.

 阅读快车系列答案
阅读快车系列答案| A. | (1,2) | B. | (2,4) | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{4},\frac{1}{2})$ |
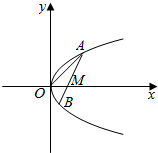 如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.
如图,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A,O,B三点作抛物线C.