题目内容
15．已知f（x）可导，且$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{2x}$=2，则f′（1）=4．分析 直接根据导数的定义f'（1）=2•$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{2x}$=4，得出结果．
解答 解：根据导数的定义得，
f'（1）=$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{1-（1-x）}$
=$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{x}$
=2•$\underset{lim}{x→0}$$\frac{f（1）-f（1-x）}{2x}$
=2×2=4，
即f'（1）=4，
故答案为：4．
点评 本题主要考查了导数的概念及其应用，涉及极限的运算及其恒等变形，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
5．已知定义在R上的奇函数f（x）满足
①对任意的x都有f（x+4）=f（x）成立；
②当x∈[0，2]时，f（x）=2-2|x-1|，
则$f（x）=\frac{1}{|x|}$在[-4，4]上根的个数是（ ）
①对任意的x都有f（x+4）=f（x）成立；
②当x∈[0，2]时，f（x）=2-2|x-1|，
则$f（x）=\frac{1}{|x|}$在[-4，4]上根的个数是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
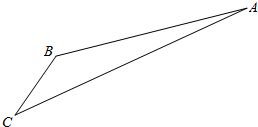如图，旅客从某旅游区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50米/分钟，在甲出发2分钟后，乙从A乘缆车到B，在B处停留1分钟后，再从B匀速步行到C．假设缆车匀速直线运动的速度为130米/分钟，山路AC长1260米，经测量，cosA=$\frac{12}{13}$，cosC=$\frac{3}{5}$．
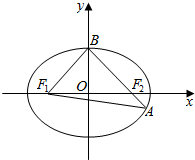如图所示，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，左，右焦点分别为F1，F2上顶点为B，延长BF2交椭圆C于点A，且△ABF1的周长为8．
20．一次考试中，给出了9道考题，要求考生完成6道题，且前五道题中至少要完成3道，则考生选题解答的选法总数是（ ）
| A． | 72 | B． | 71 | C． | 73 | D． | 74 |
如图，在四陵锥P-ABCD中，AB∥CD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：
