题目内容
19．一个项数为偶数的等比数列，所有项之和为偶数项之和的4倍，前3项之积为64．求其通项公式．分析 设此等比数列{an}有2n项，公比为q，则q≠1．由题意可得：a1a2a3=64，a1+a2+…+a2n=4（a2+a4+…+a2n），即${a}_{1}^{3}{q}^{3}$=64，$\frac{{a}_{1}（{q}^{2n}-1）}{q-1}$=$\frac{4{a}_{1}q（{q}^{2n}-1）}{{q}^{2}-1}$，化简整理即可得出．
解答 解：设此等比数列{an}有2n项，公比为q，则q≠1．
由题意可得：a1a2a3=64，a1+a2+…+a2n=4（a2+a4+…+a2n），
∴${a}_{1}^{3}{q}^{3}$=64，$\frac{{a}_{1}（{q}^{2n}-1）}{q-1}$=$\frac{4{a}_{1}q（{q}^{2n}-1）}{{q}^{2}-1}$，
化为a1q=4，q+1=4q，
解得a=$\frac{1}{3}$，a1=12．
∴an=12×$（\frac{1}{3}）^{n-1}$=4×$（\frac{1}{3}）^{n-2}$．
点评 本题考查了等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
9．长方体ABCD-A′B′C′D′的顶点均在球面上，且AB=1，AC=2，AA′=3，则该球的表面积为（ ）
| A． | 7π | B． | 14π | C． | $\frac{7π}{2}$ | D． | $\frac{7\sqrt{14}π}{3}$ |
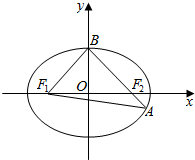如图所示，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{\sqrt{2}}{2}$，左，右焦点分别为F1，F2上顶点为B，延长BF2交椭圆C于点A，且△ABF1的周长为8．
如图，在四陵锥P-ABCD中，AB∥CD，CD=2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．求证：
11．已知$\frac{π}{2}$≤β＜α＜$\frac{3π}{4}$，sin（α+β）=-$\frac{3}{5}$，cos（α-β）=$\frac{12}{13}$，则cos2β的值为（ ）
| A． | -$\frac{63}{65}$ | B． | $\frac{63}{65}$ | C． | $\frac{33}{65}$ | D． | -$\frac{33}{65}$ |