题目内容
7.已知定义域为(-∞,+∞)的偶函数f(x)的一个单调递增区间是(2,6),关于函数y=f(2-x)①一个递减区间是(4,8)
②一个递增区间是(4,8)
③其图象对称轴方程为x=2
④其图象对称轴方程为x=-2
其中正确的序号是②③.
分析 根据条件即可判断出f(x)在(-6,-2)上递减,并且其图象关于x=0对称,这样分别解-6<2-x<-2和2-x=0即可求出函数y=f(2-x)的一个递增区间和图象的对称轴方程.
解答 解:解2<2-x<6得,-4<x<0;
解-6<2-x<-2得,4<x<8;
∵f(x)是偶函数,在(2,6)上递增;
∴f(x)在(-6,-2)上递减;
∴y=f(2-x)在(4,8)上递增;
f(x)关于y轴对称,即关于x=0对称;
解2-x=0得,x=2;
∴y=f(2-x)关于x=2对称;
即函数y=f(2-x)的对称轴为x=2;
∴②③正确.
故答案为:②③.
点评 考查偶函数的定义,偶函数图象的对称性,偶函数在对称区间上的单调性特点,以及复合函数的单调性及单调区间的求法.

练习册系列答案
相关题目
14.已知复数z,满足(z-1)i=i-1,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2+i | D. | $\sqrt{5}$ |
18.设a>b>0,a+b=1,若x=($\frac{1}{a}$)b,y=log${\;}_{(\frac{1}{a}+\frac{1}{b})}$ab,z=log${\;}_{\frac{1}{b}}$a,则x,y,z的大小关系是( )
| A. | y<x<z | B. | y<z<x | C. | x<y<z | D. | z<y<x |
2.函数y=kx+2与函数$y=\frac{1}{|x|}$的图象至少有两个公共点,关于k不等式(k-2)a-k>0有解,则实数a的取值范围是( )
| A. | $-1<a<\frac{1}{3}$ | B. | $a<\frac{1}{3}$ | C. | a<-1 | D. | a≥1 |
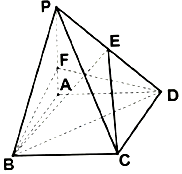 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,$2\overrightarrow{AF}=\overrightarrow{FP}$,$\overrightarrow{PE}=λ\overrightarrow{ED}$,∠ABC=60°,PA=3,AB=2.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为菱形,$2\overrightarrow{AF}=\overrightarrow{FP}$,$\overrightarrow{PE}=λ\overrightarrow{ED}$,∠ABC=60°,PA=3,AB=2.