题目内容
8.如图是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )
| A. | 在区间(-2,1)上f(x)是增函数 | B. | 在(1,3)上f(x)是减函数 | ||
| C. | 当x=4时,f(x)取极大值 | D. | 在(4,5)上f(x)是增函数 |
分析 由于f′(x)≥0⇒函数f(x)单调递增;f′(x)≤0⇒单调f(x)单调递减,观察f′(x)的图象可知,通过观察f′(x)的符号判定函数的单调性即可.
解答 解:由于f′(x)≥0⇒函数f(x)单调递增;f′(x)≤0⇒单调f(x)单调递减
观察f′(x)的图象可知,
当x∈(-2,1)时,函数先递减,后递增,故A错误
当x∈(1,3)时,函数先增后减,故B错误
当x∈(4,5)时函数递增,故D正确
由函数的图象可知函数在x=4处取得函数的极小值,故C错误
故选:D.
点评 本题主要考查了导数的应用:通过导数的符号判定函数单调性,要注意不能直接看导函数的单调性,而是通过导函数的正负判定原函数的单调性.

练习册系列答案
相关题目
19.设凸k(k≥3且k∈N)边形的对角线的条数为f(k),则凸k+1边形的对角线的条数为f(k+1)=f(k)+( )
| A. | k-1 | B. | k | C. | k+1 | D. | k2 |
20.已知奇函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x>0时有2f(x)+xf′(x)>x2,则不等式(x+2014)2f(x+2014)+4f(-2)<0的解集为( )
| A. | (-∞,-2012) | B. | (-2016,-2012) | C. | (-∞,-2016) | D. | (-2016,0) |
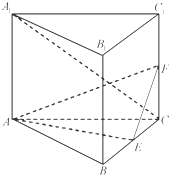 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,AA1=$\sqrt{2}$,E,F分别是BC,CC1的中点.