题目内容
3.设函数f(x)=2cos2x+2$\sqrt{3}$sinxcosx(x∈R).(1)求函数f(x)的最小正周期;
(2)在0<x≤$\frac{π}{3}$的条件下,求f(x)的取值范围.
分析 (1)利用三角恒等变换,化简函数的解析式,再利用正弦函数的周期性求得函数f(x)的最小正周期.
(2)利用定义域和值域,求得在0<x≤$\frac{π}{3}$的条件下,求f(x)的取值范围.
解答 解:(1)f(x)=2cos2x+2$\sqrt{3}$sinxcosx=cos2x+$\sqrt{3}$sin2x+1=2sin (2x+$\frac{π}{6}$)+1,
所以,函数f(x)的最小正周期为π;
(2)∵0<x≤$\frac{π}{3}$时,∴$\frac{π}{6}$<2x+$\frac{π}{6}$≤$\frac{5π}{6}$,故当2x+$\frac{π}{6}$=$\frac{5π}{6}$时 函数取得最小值为2×$\frac{1}{2}$+1=2,
故当2x+$\frac{π}{6}$=$\frac{π}{2}$时,函数取得最大值为2×1+1=3,故f(x)的值域是[2,3].
点评 本题主要考查三角恒等变换,正弦函数的周期性、定义域和值域,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.如图是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )


| A. | 在区间(-2,1)上f(x)是增函数 | B. | 在(1,3)上f(x)是减函数 | ||
| C. | 当x=4时,f(x)取极大值 | D. | 在(4,5)上f(x)是增函数 |
15.x,y∈R,若|x|+|y|+|x-1|+|y-1|≤2,则x+y的取值范围为( )
| A. | [-2,0] | B. | [0,2] | C. | [-2,2] | D. | (0,2) |
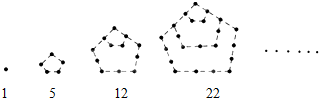 如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.
如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则an=$\frac{{3{n^2}-n}}{2}$.