题目内容
12．
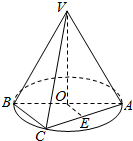如图AB是圆O的直径，点C是圆O上不同于A，B的一点，点V是圆O所在平面外一点．（Ⅰ）若点E是AC的中点，求证：OE∥平面VBC；
（Ⅱ）若VA=VB=VC=AB，求直线VC与平面ABC所成角．
分析 （Ⅰ）由三角形中位线定理得OE∥BC，由此能证明OE∥平面VBC．
（Ⅱ）连接OC，推导出∠VCO为直线VC与平面ABC所成角，由此能求出直线VC与平面ABC所成角．
解答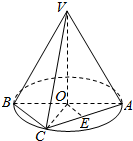 
证明：（Ⅰ）在△ABC中，∵O、E分为AB、AC中点，
∴OE∥BC，…（2分）
又∵OE?平面VBC，BC?平面VBC，
∴OE∥平面VBC…（5分）
解：（Ⅱ）连接OC，∵O为AB的中点，且VA=VB，
∴VO⊥AB，…（7分）
又∵VB=VC、OB=OC，∴△VOB≌△VOC，
∴VO⊥OC，∴VO⊥平面ABC，…（9分）
∴∠VCO为直线VC与平面ABC所成角，…（10分）
∵VC=AB=2OC，∴∠VCO=60°．
∴直线VC与平面ABC所成角为60°…（12分）
点评 本题考查线面平行的证明，考查线面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
11．下列关于正弦定理的叙述中错误的是（ ）
| A． | 在△ABC中，a：b：c=sinA：sinB：sinC | |
| B． | 在△ABC中，若sin2A=sin2B，则A=B | |
| C． | 在△ABC中，若sinA＞sinB，则A＞B；若A＞B，则sinA＞sinB | |
| D． | 在△ABC中，$\frac{a}{sinA}$=$\frac{b+c}{sinB+sinC}$ |
7．设a=20.3，b=log20.3，c=0.32，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | c＞a＞b | D． | b＞c＞a |