题目内容
1.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,$\overrightarrow{a}$($\overrightarrow{b}-\overrightarrow{a}$)=-3,则向量$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{1}{2}$.分析 根据平面向量的数量积运算性质计算$\overrightarrow{a}•\overrightarrow{b}$,得出cos<$\overrightarrow{a},\overrightarrow{b}$>,再代入投影公式计算.
解答 解:∵${\overrightarrow{a}}^{2}$=4,$\overrightarrow{a}$($\overrightarrow{b}-\overrightarrow{a}$)=$\overrightarrow{a}•\overrightarrow{b}$-${\overrightarrow{a}}^{2}$=-3,
∴$\overrightarrow{a}•\overrightarrow{b}$=1,
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{1}{2|\overrightarrow{b}|}$,
∴$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为|$\overrightarrow{b}$|cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
12.函数f(x)=x2-2x+3的值域是( )
| A. | (-∞,2] | B. | (0,+∞) | C. | [2,+∞) | D. | [0,2] |
6.点P(1,-1)到直线ax+3y+2a-6=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
10.在△ABC中,内角A,B,C所对的边分别是a,b,c.已知b=26,c=15,C=28°,则△ABC有( )
| A. | 一解 | B. | 二解 | C. | 无解 | D. | 不能确定 |
11.若“x=1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则实数a的取值范围是( )
| A. | [-1,+∞) | B. | (-1,1) | C. | [-1,1] | D. | (-∞,1] |
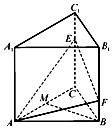 三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.