Question

11．如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，PD=DC=a，E是PC的中点．
（1）求四棱锥P-ABCD的体积；
（2）求直线PB与平面ABCD所成角的正切值；
（3）证明：PA∥平面EDB．

Answer 1

分析 （1）由PD⊥底面ABCD，底面ABCD是正方形，PD=DC=a，能求出四棱锥P-ABCD的体积．
（2）由PD⊥底面ABCD，知直线PB与平面ABCD所成角为∠PBD，由此能求出直线PB与平面ABCD所成角的正切值．
（3）连结AC交BD于O，连结EO，推导出PA∥EO，由此能证明PA∥平面EDB．

解答 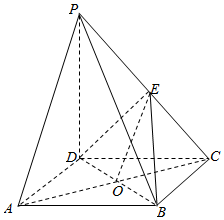解：（1）∵PD⊥底面ABCD，底面ABCD是正方形，PD=DC=a，
∴四棱锥P-ABCD的体积${V_{P-ABCD}}=\frac{1}{3}{S_{ABCD}}•PD=\frac{1}{3}×a×a×a=\frac{1}{3}{a^3}$．…4分
（2）由PD⊥底面ABCD，知直线PB与平面ABCD所成角为∠PBD，…6分
∵$BD=\sqrt{2}a$，
∴$tan∠PBD=\frac{a}{{\sqrt{2}a}}=\frac{{\sqrt{2}}}{2}$，
∴直线PB与平面ABCD所成角的正切值为$\frac{\sqrt{2}}{2}$．…8分
证明：（3）连结AC交BD于O，连结EO，
∵底面ABCD是正方形，∴点O是AC的中点，
在△PAC中，∵E是PC的中点，∴EO是中位线，
∴PA∥EO，
∵EO?平面EBD，且PA?平面EBD，
∴PA∥平面EDB．…12分

点评 本题考查四棱锥的体积的求法，考查线面角的正切值的求法，考查线面平行的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．